В задаче о диете в правой части ограничений находятся
К задачам оптимизации относятся задачи на отыскание
—целевой функции
+ максимума или минимума целевой функции
—решения системы уравнений
— решения системы неравенств
Критерием оптимальности задачи математического программирования является
+целевая функция
—система уравнений
—система неравенств
—условие неотрицательности переменных
Общая задача линейного программирования имеет вид
— (max или min), ,
—
— (max или min),
+ (max или min), , ,
Задача математического программирования является задачей линейного программирования, если
—целевая функция является линейной, а система ограничений нелинейная
—система ограничений – это система линейных уравнений или неравенств, а целевая функция нелинейная
+целевая функция является линейной, а система ограничений – система линейных уравнений или неравенств
—условие неотрицательности переменных – линейно
Задача математического программирования является задачей нелинейного программирования, если
—условие неотрицательности переменных нелинейно
+ целевая функция является нелинейной
—целевая функция является линейной
— условие неотрицательности переменных не выполняется
Задача нелинейного программирования называется квадратичной, если
—
—
+
—
Задача нелинейного программирования называется задачей дробно – линейного программирования, если
—
—
—
+
Задача математического программирования называется задачей целочисленного программирования, если
—все коэффициенты целевой функции – целые числа
—все коэффициенты системы ограничений – целые числа
—все – целые числа
+все – целые числа,
Абстрактное отображение реального экономического процесса с помощью математических выражений, уравнений, неравенств – это
—система ограничений
— целевая функция
+экономико–математическая модель
—условие неотрицательных переменных
Любая экономико – математическая модель задачи линейного программирования состоит из
—целевой функции и системы ограничений
+целевой функции, системы ограничений и условия неотрицательности переменных
—системы ограничений и условия неотрицательности переменных
— целевой функции и условия неотрицательности переменных
Задача математического программирования называется задачей сепарабельного программирования, если целевая функция равна
+
—
— , где
—
Оптимальное решение задачи математического программирования – это
— допустимое решение системы ограничений
—любое решение системы ограничений
+допустимое решение системы ограничений, приводящее к максимуму или минимуму целевой функции
—максимальное или минимальное решение системы ограничений
Если целевая функция ,то задача математического программирования является задачей
—линейного программирования
— целочисленного программирования
—дробно – линейного программирования
+квадратичного программирования
Динамическое программирование – это математический аппарат, позволяющий
+ осуществить оптимальное планирование многошаговых управляемых процессов
—исследовать динамику функции
—оказывать влияние на развитие процесса
—наблюдать процесс в его развитии
Если целевая функция , то задача математического программирования, называется задачей
—линейного программирования
— квадратичного программирования
+дробно – линейного программирования
— дробно – квадратичного программирования
Все ограничения в задаче математического программирования должны быть
— одинакового смысла
—противоречивы
+непротиворечивы
—противоположного смысла
Задачи линейного программирования предполагают
—минимальные ресурсы
— максимальные ресурсы
—неограниченные ресурсы
+ограниченные ресурсы
В задаче об оптимальном распределении ресурсов критерием оптимальности является
+максимальная прибыль
—минимальная прибыль
—максимальные издержки
—минимальные издержки
В задаче «о диете» критерием оптимальности является
—максимальная прибыль
— минимальная прибыль
—максимальная стоимость рациона питания
+минимальная стоимость рациона питания
Задачи об оптимальном распределении ресурсов и «о диете» относятся к задачам
+линейного программирования
—нелинейного программирования
— динамического программирования
—целочисленного программирования
Система ограничений называется стандартной, если она содержит все знаки
—³
+£
—=
—¹
Задача линейного программирования решается графическим способом, если в задаче
—одна переменная
+две переменные
—три переменные
—четыре переменные
Неравенство вида описывает
—прямую
—окружность
+полуплоскость
—плоскость
Областью допустимых решений ЗЛП является
—вся плоскость
—круг
+выпуклый многоугольник
—координатные оси
Максимум или минимум целевой функции находится
—в начале координат
—на сторонах выпуклого многоугольника решений
—внутри выпуклого многоугольника решений
+в вершинах выпуклого многоугольника решений
Каноничкеским видом ЗЛП называется такой ее вид, в котором система ограничений содержит знаки
—³
— £
+=
—¹
Для приведения ЗЛП к каноническому виду вводятся
+дополнительные переменные
—искусственные переменные
—отрицательные переменные
—нулевые переменные
Если ограничение задано со знаком «³», то дополнительная переменная вводится в это ограничение с коэффициентом
—+1
+-1
—0
—М
Если ограничение задано со знаком «£», то дополнительная переменная вводится в это ограничение с коэффициентом
++1
—-1
—0
—М
В целевую функцию дополнительные переменные вводятся с коэффициентами
— +1
—-1
+0
—M
В задаче об оптимальном распределении ресурсов дополнительная переменная имеет экономический смысл:
—прибыль от реализации продукции i –го вида
—прибыль от реализации 1 единицы продукции i – го вида
—использованные ресурсы i – го вида
+неиспользованные ресурсы i –го вида
В задаче об оптимальном распределении ресурсов коэффициент целевой функции – это
—прибыль от реализации продукции j – го вида
+ прибыль от реализации 1 единицы продукции j– го вида
—количество продукции j – го вида
—расход сырья для производства продукции j – го вида
В задаче об оптимальном распределении ресурсов переменная целевой функции – это
—прибыль от реализации продукции j – го вида
— прибыль от реализации 1 единицы продукции j– го вида
+количество продукции j – го вида
—расход сырья для производства продукции j – го вида
В задаче «о диете» коэффициент – целевой функции – это
+цена 1 единицы продукта j– го вида
— расход продукта j – го вида
— прибыль от использования продукта j– го вида
— прибыль от реализации продукта j– го вида
В задаче «о диете» коэффициент – это
+содержание питательного вещества с номером i в 1 единице j – го продукта
—цена 1 единицы продукта j– го вида
—количество j – го продукта, необходимого i – му животному
—издержки на приобретение j – го продукта для прокорма i – го животного
В задаче об оптимальном распределении ресурсов коэффициент – это
+количество ресурса с номером , необходимого для изготовления 1 единицы продукции j – го вида
—неиспользованные ресурсы i– го вида
—прибыль от реализации 1 единицы продукции j – го вида
—количество продукции j – го вида
В задаче об оптимальном распределении ресурсов требование неотрицательности накладывается на
—только основные переменные
+на основные и дополнительные переменные
—только на дополнительные переменные
—первую и вторую переменные
В задаче о «диете» область допустимых решений
—ограничена
—незамкнута
+неограничена
—невыпукла
Динамическое программирование основано на решении
—вероятностного уравнения
—дифференциального уравнения
—уравнение регрессии
+функционального уравнения
В задаче о «диете» в правой части ограничений находятся
+ необходимое количество питательных веществ каждого вида
—стоимость единицы корма j – го вида
—количества корма каждого вида
—общая стоимость рациона
Источник
К задачам оптимизации относятся задачи на отыскание
+—максимума или минимума целевой функции
Критерием оптимальности задачи математического программирования является
+—целевая функция
Общая задача линейного программирования имеет вид
+— (max или min), , ,
Задача математического программирования является задачей линейного программирования, если
—целевая функция является линейной, а система ограничений – система линейных уравнений или неравенств
Задача математического программирования является задачей нелинейного программирования, если
+—целевая функция является нелинейной
Задача нелинейного программирования называется квадратичной, если
+—
Задача нелинейного программирования называется задачей дробно – линейного программирования, если
+—
Задача математического программирования называется задачей целочисленного программирования, если
+—все – целые числа,
Абстрактное отображение реального экономического процесса с помощью математических выражений, уравнений, неравенств – это
+—экономико–математическая модель
Любая экономико – математическая модель задачи линейного программирования состоит из
+—целевой функции, системы ограничений и условия неотрицательности переменных
Задача математического программирования называется задачей сепарабельного программирования, если целевая функция равна
+—
Оптимальное решение задачи математического программирования – это
+—допустимое решение системы ограничений, приводящее к максимуму или минимуму целевой функции
Если целевая функция , то задача математического программирования является задачей
+—квадратичного программирования
Динамическое программирование – это математический аппарат, позволяющий
+—осуществить оптимальное планирование многошаговых управляемых процессов
Если целевая функция , то задача математического программирования, называется задачей
+—дробно – линейного программирования
Все ограничения в задаче математического программирования должны быть
+—непротиворечивы
Задачи оптимального использования ресурсов предполагают
+—ограниченные ресурсы
В задаче об оптимальном распределении ресурсов критерием оптимальности является
+—максимальная прибыль
В задаче «о диете» критерием оптимальности является
+—минимальная стоимость рациона питания
Задачи об оптимальном распределении ресурсов и «о диете» относятся к задачам
+—линейного программирования
В задаче наилучшего использования ресурсов система ограничений называется стандартной, если она содержит все знаки
+—£
Задача линейного программирования решается графическим способом, если в задаче
+—две переменные
Неравенство вида описывает
+—полуплоскость
Областью допустимых решений ЗЛП является
+—выпуклый многогранник
Максимум или минимум целевой функции находится
+—в вершинах выпуклого многоугольника решений
Каноническим видом ЗЛП называется такой ее вид, в котором система ограничений содержит знаки
+—=
Для приведения ЗЛП к каноническому виду вводятся
+—дополнительные переменные
Если ограничение задано со знаком «³», то дополнительная переменная вводится в это ограничение с коэффициентом
+—-1
Если ограничение задано со знаком «£», то дополнительная переменная вводится в это ограничение с коэффициентом
+—+1
В целевую функцию дополнительные переменные вводятся с коэффициентами
+—0
В задаче об оптимальном распределении ресурсов дополнительная переменная имеет экономический смысл:
+—неиспользованные ресурсы i –го вида
В задаче об оптимальном распределении ресурсов коэффициент целевой функции – это
+—прибыль от реализации 1 единицы продукции j– го вида
В задаче об оптимальном распределении ресурсов переменная целевой функции – это
+—количество продукции j – го вида
В задаче «о диете» коэффициент – целевой функции – это
+—цена 1 единицы продукта j– го вида
В задаче «о диете» коэффициент – это
+—содержание питательного вещества с номером i в 1 единице j – го продукта
В задаче об оптимальном распределении ресурсов коэффициент – это
+—норма расхода сырья i – го вида для производства 1 единицы продукции j – го вида
В задаче «о диете» – это
+—суточная норма j – го продукта, необходимая одному животному
В задаче об оптимальном распределении ресурсов целевая функция – это
+—суммарная прибыль от реализации произведенной продукции
В задаче «о диете» целевая функция – это
+—суммарные издержки на приобретение суточного рациона питания
В задаче «о диете» свободные члены системы ограничений – это
+—минимальное количество i – го питательного вещества, необходимое одному животному в сутки
В задаче об оптимальном распределении ресурсов свободные члены системы ограничений – это
+—запасы i – го вида сырья
В задаче о «диете» число ограничений равно
+—числу видов питательных веществ, необходимых каждому животному
В задаче об оптимальном распределении ресурсов число ограничений равно
+—числу видов ресурсов
В задаче о «диете» число дополнительных переменных равно
+—числу видов питательных веществ
В задаче об оптимальном использовании ресурсов число дополнительных переменных равно
+—числу видов ресурсов
Экономико – математическая модель задачи об оптимальном распределении ресурсов в матричной форме имеет вид:
+—
Экономико – математическая модель задачи об оптимальном рационе питания в матричной форме имеет вид:
+—
Дана задача линейного программирования
| Виды сырья | Нормы расхода сырья | Запасы сырья |
| Изделие 1-го вида | Изделие 2-го вида | Изделие 3-го вида |
| S1 S2 S3 | ||
| Прибыль от реализации 1-го изделия |
Целевая функция и целевая установка этой ЗЛП имеют вид:
+—
Дана задача линейного программирования
| Виды сырья | Нормы расхода сырья | Запасы сырья |
| Изделие 1-го вида | Изделие 2-го вида | Изделие 3-го вида |
| S1 S2 S3 | ||
| Прибыль от реализации 1-го изделия |
Первое ограничение системы ограничений имеет вид:
+—
Дана задача линейного программирования
| Виды питательных веществ | Содержание питательного вещества в 1 ед. продукции | Минимальная суточная потребность в питательном веществе |
| 1-го вида | 2-го вида | 3-го вида |
| Белки Жиры Углеводы | ||
| Цена 1 ед. продукта |
Целевая функция и целевая установка этой ЗЛП имеют вид:
+—
Дана задача линейного программирования
| Виды питательных веществ | Содержание питательного вещества в 1 ед. продукции | Минимальная суточная потребность в питательном веществе |
| 1-го вида | 2-го вида | 3-го вида |
| Белки Жиры Углеводы | ||
| Цена 1 ед. продукта |
Третье ограничение системы ограничений имеет вид:
+—
Система ограничений задачи линейного программирования имеет вид:
.
Многоугольник допустимых решений имеет вид выпуклого
+—четырехугольника
Система ограничений задачи линейного программирования имеет вид:
.
Многоугольник допустимых решений имеет вид выпуклого
+—треугольника
Система ограничений задачи линейного программирования имеет вид:
.
Многоугольник допустимых решений имеет вид выпуклого
+—пятиугольника
Дана ЭММ задачи линейного программирования:
,
.
Оптимальный план данной ЗЛП достигается в точке с координатами
+—
Дана ЭММ задачи линейного программирования:
,
.
Минимум целевой функции достигается в точке с координатами +—
Источник
2.1. Задача о диете
Исторические задача о диете является одной из первых задач линейного
программирования.
Постановка задачи – первый и наиболее важный этап построения модели,
способный обеспечить правильное решение проблемы.
Даме необходимо похудеть, за помощью обратилась к подруге.
Построение модели – рассмотрение этого этапа и является главной целью.
Подруга посоветовала перейти на рациональное питание, состоящее из двух
продуктов P и Q.
Суточное питание этими продуктами должно давать не более 14 единиц жира
(чтобы похудеть), но не менее 300 калорий. На упаковке продукта Р
написано, что в одном килограмме этого продукта содержится 15 единиц жира и 150
калорий, а на упаковке с продуктом Q – 4
единицы жира и 200 калорий соответственно. При этом цена 1 килограмма продукта
Р равна 15 руб., а 1 кг продукта Q – 25
руб.
Так как дама была стеснена в средствах, но ее интересовал вопрос: в какой
пропорции нужно брать эти продукты для того, чтобы выдержать условия диеты и
истратить как можно меньше денег?
Перейдем к формализации данной ситуации на языке математических символов.
Обозначим через х количество продукта Р и
через у количество продукта Q, требуемые
для выполнения условий диеты.
Количество единиц жира, содержащегося в х кг продукта
Р и в у кг продукта Q, равно
15х + 4 и по условию диеты не должно превосходить 14:
В свою очередь, количество калорий, содержащихся в х
кг продукта Р и в у кг продукта Q,
равно 150х + 200у и по условию диеты должно быть не меньше 300:
Теперь о стоимости z продуктов.
Она равна
и в соответствии с высказанными пожеланиями должна быть минимальной.
Последнее записывается так:
Тем самым мы получили систему формул:
которую решим графическим способом.
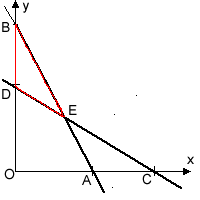
Нас интересует только та ее часть, которая лежит над треугольником
BDE. Вычисляя значения z
во всех трех вершинах этого треугольника
и сравнивая полученные результаты, замечаем, что наименьшее значение (35)
достигается в вершине Е. Таким образом,
и искомая пропорция – 2 : 3.
2.2. Задача о выпуске продукции
Фирма выпускает два вида древесно-стружечных плит – обычные и
улучшенные. При этом производится две основные операции – прессование и отделка.
Требуется указать, какое количество плит каждого типа можно изготовить в течение
месяца так, чтобы обеспечить максимальную прибыль при следующих ограничениях на
ресурсы (материал, время, затраты):
Затраты | Партия из 100 плит | Имеющиеся ресурсы на месяц | |
обычных | улучшенных | ||
| Материал (фунты) Время на прессование (часы) Время на отделку (часы) Средства (деньги) | 20 | 40 | 4000 |
| Прибыль | 80 | 100 | max |
Перейдем к построению математической модели
поставленной задачи. Введем следующие обозначения. Пусть
х – количество партий в 100 плит обычного
вида, изготавливаемых в течение месяца;
у – количество партий в 100 плит
улучшенного качества, изготавливаемых в течение месяца.
Тогда ожидаемую прибыль можно записать так:
Требуется найти такие значения х и у,
подчиненные условиям
для которых
Для того, чтобы найти в первой четверти плоскости хОу
множество точек, координаты (х, у) которых удовлетворяют указанным выше
неравенствам, необходимо сначала построить прямые (по точкам их пересечения с
координатными осями)
а затем, используя точку начала отсчета О(0, 0),
определить соответствующие полуплоскости. Пересечением полученных полуплоскостей
будет четырехугольник ОВМЕ.
Наша целевая функция достигает наибольшего значения в одной
из вершин четырехугольника.
Нам необходимо найти координаты точки М – точки
пересечения прямых EF и АВ, для этого надо
решить систему уравнений
Вычислить значения z в точках
В(0, 100), Е(150, 0), М(100, 50):
Из полученных значений выберем наибольшее и получим ответ:
2.3. Общая задача линейного программирования
В общем случае и число неизвестных , и число ограничений
могут достигать десятков, сотен, тысяч и т.д. Однако набор соответствующих
условий ничем (кроме количества) от рассмотренных выше примеров не отличается.
Это нетрудно заметить уже по общей постановке задачи линейного программирования.
Стандартная математическая формулировка общей задачи
линейного программирования выглядит так: требуется найти экстремальное значение
показателя эффективности (целевой функции)
(линейной функции элементов решения
) при линейных ограничительных
условиях, накладываемых на элементы решения:
где – заданные числа.
Что касается существующих методов решения этой задачи с
числом переменных, больших двух, то в их основе лежат те же идеи, на которые мы
опирались при разработке графического подхода. Конечно, в случае сильного
увеличения числа переменных и ограничений техника получения решения заметно
усложняется, но она опирается на совершенно стандартные, хорошо разработанные
алгоритмы (возникающие трудности связаны лишь с ростом объема необходимых
вычислений).
Общую постановку задачи линейного программирования можно
записать в более компактной форме, если воспользоваться следующим правилом.
Правило сокращенного суммирования. Для обозначения
суммы чисел :
принята такая запись:
где ∑ – знак суммирования, а
k – индекс суммирования.
Это обозначение очень удобно:
А вот как выглядит запись общей задачи линейного
программирования:
2.4. Транспортная задача
Важный тип задач линейного программирования представляет
задача о перевозках. Называется она так потому, что цель этой задачи
заключается в минимизации полной стоимости перевозок известного количества
товаров со складов к потребителю.
Сбалансированная задача – задача о перевозках, в
которой общий объем товаров, готовых к отправлению, в точности равен объему
товаров, который готовы принять в пунктах назначения.
Пример 1. Рассмотрим транспортную задачу, заданную таблицей
| В | Наличие | |||
| 1 | 2 | |||
| А | 1 2 | 1 2 | 2 1 | 20 10 |
| Запрос | 16 | 14 | 30 | |
Решение. Пусть – искомое число единиц
товара, пересылаемого из пункта в пункт
. Тогда данные таблицы можно
представить в следующем виде:
при условии, что
Положим и выразим через
t остальные переменные:
из первого уравнения: ,
из второго уравнения: ,
из третьего уравнения:
Тогда
Из того, что все не
отрицательны, получаем, что переменная t должна
удовлетворять одновременно следующим четырем неравенствам:
Тем самым, мы получили условие .
Не трудно заметить, что при
t = 16.
Ответ:
| В | Наличие | ||||
| 1 | 2 | 3 | |||
| А | 1 | 8 | 5 | 6 | 120 |
| 2 | 4 | 9 | 7 | 180 | |
| Запрос | 70 | 140 | 90 | 300 | |
Пример 2. Компания имеет два товарных склада и трех оптовых
покупателей. Известно, что общий объем запасов на складах составляет 300 тыс.
единиц продукции и совпадает с общим объемом заказов покупателей.
Обозначим через количество товара,
поставляемого со склада покупателю
.
Тогда соответствующая транспортная задача может быть
сформулирована следующим образом.
Минимизировать общую стоимость перевозок:
при условии, что
Получаем задачу линейного программирования, в которой
основные ограничения вследствие того, что транспортная задача сбалансирована,
является равенствами.
Положим и
выразим через u и
v остальные переменные. Имеем
Учитывая, что все перевозки должны получить неотрицательные значения, мы
приходим к задаче
которую можно решить графическим методом.
Выписанные неравенства определяют на плоскости (u,
v) пятиугольник с вершинами (30, 0), (70, 0), (70, 50), (0,
120), (0, 30).
Ответ:
В начало
Источник
