В задаче о диете число переменных равно числу
К задачам оптимизации относятся задачи на отыскание
+—максимума или минимума целевой функции
Критерием оптимальности задачи математического программирования является
+—целевая функция
Общая задача линейного программирования имеет вид
+— (max или min), , ,
Задача математического программирования является задачей линейного программирования, если
—целевая функция является линейной, а система ограничений – система линейных уравнений или неравенств
Задача математического программирования является задачей нелинейного программирования, если
+—целевая функция является нелинейной
Задача нелинейного программирования называется квадратичной, если
+—
Задача нелинейного программирования называется задачей дробно – линейного программирования, если
+—
Задача математического программирования называется задачей целочисленного программирования, если
+—все – целые числа,
Абстрактное отображение реального экономического процесса с помощью математических выражений, уравнений, неравенств – это
+—экономико–математическая модель
Любая экономико – математическая модель задачи линейного программирования состоит из
+—целевой функции, системы ограничений и условия неотрицательности переменных
Задача математического программирования называется задачей сепарабельного программирования, если целевая функция равна
+—
Оптимальное решение задачи математического программирования – это
+—допустимое решение системы ограничений, приводящее к максимуму или минимуму целевой функции
Если целевая функция , то задача математического программирования является задачей
+—квадратичного программирования
Динамическое программирование – это математический аппарат, позволяющий
+—осуществить оптимальное планирование многошаговых управляемых процессов
Если целевая функция , то задача математического программирования, называется задачей
+—дробно – линейного программирования
Все ограничения в задаче математического программирования должны быть
+—непротиворечивы
Задачи оптимального использования ресурсов предполагают
+—ограниченные ресурсы
В задаче об оптимальном распределении ресурсов критерием оптимальности является
+—максимальная прибыль
В задаче «о диете» критерием оптимальности является
+—минимальная стоимость рациона питания
Задачи об оптимальном распределении ресурсов и «о диете» относятся к задачам
+—линейного программирования
В задаче наилучшего использования ресурсов система ограничений называется стандартной, если она содержит все знаки
+—£
Задача линейного программирования решается графическим способом, если в задаче
+—две переменные
Неравенство вида описывает
+—полуплоскость
Областью допустимых решений ЗЛП является
+—выпуклый многогранник
Максимум или минимум целевой функции находится
+—в вершинах выпуклого многоугольника решений
Каноническим видом ЗЛП называется такой ее вид, в котором система ограничений содержит знаки
+—=
Для приведения ЗЛП к каноническому виду вводятся
+—дополнительные переменные
Если ограничение задано со знаком «³», то дополнительная переменная вводится в это ограничение с коэффициентом
+—-1
Если ограничение задано со знаком «£», то дополнительная переменная вводится в это ограничение с коэффициентом
+—+1
В целевую функцию дополнительные переменные вводятся с коэффициентами
+—0
В задаче об оптимальном распределении ресурсов дополнительная переменная имеет экономический смысл:
+—неиспользованные ресурсы i –го вида
В задаче об оптимальном распределении ресурсов коэффициент целевой функции – это
+—прибыль от реализации 1 единицы продукции j– го вида
В задаче об оптимальном распределении ресурсов переменная целевой функции – это
+—количество продукции j – го вида
В задаче «о диете» коэффициент – целевой функции – это
+—цена 1 единицы продукта j– го вида
В задаче «о диете» коэффициент – это
+—содержание питательного вещества с номером i в 1 единице j – го продукта
В задаче об оптимальном распределении ресурсов коэффициент – это
+—норма расхода сырья i – го вида для производства 1 единицы продукции j – го вида
В задаче «о диете» – это
+—суточная норма j – го продукта, необходимая одному животному
В задаче об оптимальном распределении ресурсов целевая функция – это
+—суммарная прибыль от реализации произведенной продукции
В задаче «о диете» целевая функция – это
+—суммарные издержки на приобретение суточного рациона питания
В задаче «о диете» свободные члены системы ограничений – это
+—минимальное количество i – го питательного вещества, необходимое одному животному в сутки
В задаче об оптимальном распределении ресурсов свободные члены системы ограничений – это
+—запасы i – го вида сырья
В задаче о «диете» число ограничений равно
+—числу видов питательных веществ, необходимых каждому животному
В задаче об оптимальном распределении ресурсов число ограничений равно
+—числу видов ресурсов
В задаче о «диете» число дополнительных переменных равно
+—числу видов питательных веществ
В задаче об оптимальном использовании ресурсов число дополнительных переменных равно
+—числу видов ресурсов
Экономико – математическая модель задачи об оптимальном распределении ресурсов в матричной форме имеет вид:
+—
Экономико – математическая модель задачи об оптимальном рационе питания в матричной форме имеет вид:
+—
Дана задача линейного программирования
| Виды сырья | Нормы расхода сырья | Запасы сырья |
| Изделие 1-го вида | Изделие 2-го вида | Изделие 3-го вида |
| S1 S2 S3 | ||
| Прибыль от реализации 1-го изделия |
Целевая функция и целевая установка этой ЗЛП имеют вид:
+—
Дана задача линейного программирования
| Виды сырья | Нормы расхода сырья | Запасы сырья |
| Изделие 1-го вида | Изделие 2-го вида | Изделие 3-го вида |
| S1 S2 S3 | ||
| Прибыль от реализации 1-го изделия |
Первое ограничение системы ограничений имеет вид:
+—
Дана задача линейного программирования
| Виды питательных веществ | Содержание питательного вещества в 1 ед. продукции | Минимальная суточная потребность в питательном веществе |
| 1-го вида | 2-го вида | 3-го вида |
| Белки Жиры Углеводы | ||
| Цена 1 ед. продукта |
Целевая функция и целевая установка этой ЗЛП имеют вид:
+—
Дана задача линейного программирования
| Виды питательных веществ | Содержание питательного вещества в 1 ед. продукции | Минимальная суточная потребность в питательном веществе |
| 1-го вида | 2-го вида | 3-го вида |
| Белки Жиры Углеводы | ||
| Цена 1 ед. продукта |
Третье ограничение системы ограничений имеет вид:
+—
Система ограничений задачи линейного программирования имеет вид:
.
Многоугольник допустимых решений имеет вид выпуклого
+—четырехугольника
Система ограничений задачи линейного программирования имеет вид:
.
Многоугольник допустимых решений имеет вид выпуклого
+—треугольника
Система ограничений задачи линейного программирования имеет вид:
.
Многоугольник допустимых решений имеет вид выпуклого
+—пятиугольника
Дана ЭММ задачи линейного программирования:
,
.
Оптимальный план данной ЗЛП достигается в точке с координатами
+—
Дана ЭММ задачи линейного программирования:
,
.
Минимум целевой функции достигается в точке с координатами +—
Источник
-: минимизировать количество потребляемых продуктов
-: максимизировать количество питательных веществ в продуктах питания
-: максимизировать прибыль
+: минимизировать издержки на рацион питания
I:
S: При преобразовании задачи линейного программирования к каноническому виду, дополнительные переменные вводятся в целевую функцию с коэффициентами,
+: равными нулю
-: равными очень большим положительным числам
-: равными правым частям соответствующих ограничений
-: равными единице
I:
S: Задача линейного программирования
max Z = С ∙ X
А1х1 + … + Аn ∙ хn = А0, X 0
задана
-: в общей форме
-: в скалярной форме
+: в векторной форме
-: в стандартной форме
I:
S: Для задачи о наилучшем использовании ресурсов дополнительные переменные показывают:
+: величину неиспользованного ресурса
-: величину ресурса, использованного в оптимальном плане
-: дополнительную прибыль от сэкономленного ресурса
-: стоимость соответствующего потребляемого ресурса
I:
S: Для задачи о смесях дополнительная переменная показывает:
-: потребление соответствующего питательного вещества в пределах нормы
+: потребление соответствующего питательного вещества в оптимальном плане сверх нормы
-: стоимость соответствующего потребляемого вещества
-: величину ресурса, использованного в оптимальном плане
I:
S: В задаче о рационе требуется:
+: минимизация общей стоимости всех кормов
-: максимизация содержания питательных веществ в кормах
-: минимизация количества кормов
-: минимизация стоимости всех питательных веществ
I:
S: Если какая-то переменная хк задачи ЛП не подчинена условию не отрицательности, то ее следует:
-: исключить из числа переменных
+: заменить двумя неотрицательными переменными, приняв хк = uk – vk
-: увеличить в два раза
-: обнулить
I:
S: Пусть х* – оптимальный план задачи ЛП на max с целевой функцией F. Тогда для любого допустимого плана х выполняется соотношение:
-: F (x) = F (x*)
-: F (x) > F (x*)
+: F (x) ≤ F (x*)
-: F (x) = –F (x*)
I:
S: Если х* – оптимальный план задачи ЛП на min, F – целевая функция, а x– любой допустимый план задачи, то справедливо следующее соотношение:
+: F (x) ≥ F (x*)
-: F (x*) + F (x) = 0
-: F (x*) ∙ F (x) = 1
-: F (x) = F (x*)
I:
S: Линейное программирование это
-: один из приемов разработки программного обеспечения ЭВМ
+: математический метод оптимизации
-: определение последовательности действий при проведении общественных мероприятий
-: составление программ линейной структуры
I:
S: В линейном программировании используются функции, уравнения и неравенства
-: преимущественно линейные
+: только линейные
-: любые
-: в зависимости от решаемой задачи
I:
S: Методы линейного программирования позволяют определить оптимальное экономическое решение
-: всегда
+: да, если оно существует
-: линейное программирование предназначено для других целей
I:
S: Конкретный план в линейном программировании представляется
-: датами
+: числовыми значениями
-: интегральной кривой возможных потерь
-: кривыми спроса
I:
S: Оптимальный план задачи ЛП это
-: любой план
-: любой допустимый план
+: допустимый план, которому соответствует максимум выручки
-: любой опорный план
I:
S: Система ограничений задачи ЛП это система
-: нестрогих неравенств
-: только строгих неравенств
-: только равенств
+: равенств и неравенств
I:
S: Допустимыми являются планы
-: любые
-: любые с положительными значениями
+: удовлетворяющие системе ограничений
-: любые с ненулевыми значениями
I:
S: Целевая функция задачи линейного программирования должна быть
-: нелинейной
+: линейной
-: любой
-:выпуклой
I
S: Математическая модель задачи линейного программирования это
-: целевая функция
+: целевая функция и набор ограничений
-: набор ограничений
I:
S: Методом линейного программирования решаются задачи поиска экстремума
-: нелинейной функции при линейных ограничениях
-: линейной функции при нелинейных ограничениях;
+: линейной функции при линейных ограничениях.
I:
S: Допустимым планом задачи является
-: любой план
+: любой план, обеспечивающий выполнение ограничений
-: это зависит от конкретного содержания задачи
-: любой план с ненулевыми значениями
S: Оптимальным планом задачи является план
-: любой, обеспечивающий выполнение ограничений
-: доставляющий экстремум целевой функции
+: доставляющий экстремум целевой функции при выполнении ограничений
-: любой с ненулевыми значениями
I:
S: В задаче линейного программирования допустимо количество ограничений
+: не более числа переменных
-: равное числу переменных
-: любое
-: не более 1000
I:
S: Максимальное значение функции при ограничениях
равно
-: 8
-: 5
+: 6
-: 1
I:
S: Максимальное значение функции при ограничениях
равно
-: 0
-: -1
-: -2
+: -3
I:
S: Максимальное значение функции при ограничениях
равно
-: 12
-: 14
+: 16
-: 18
I:
S: Максимальное значение функции при ограничениях
равно
-: 23
-: 6
+: 22
-: 14
I:
S: Максимальное значение функции при ограничениях
равно
-: 14
-: 16
-: 22
+: 30
I:
S: Для изготовления изделий и склад может отпустить металла не более 80 кг, причем на одно изделие расходуется 2 кг, а на изделие – 1кг металла. Укажите план производства, при котором обеспечен наибольший доход, если изделий требуется изготовить не более 30 шт., а изделий – не более40 шт., причем одно изделие стоит 5 ден.ед., а одно изделие -3 ден.ед.
+:
-:
-:
-:
-:
I:
S: Если вся выпускаемая продукция или ее часть реализуется комплектами, то в модели задачи необходимо изменить
-: целевую функцию и систему ограничений
-: только целевую функцию
+: только систему ограничений
I:
S: Если предприятие может пополнять объемы ресурсов, неся связанные с этим затраты, но и расширяя свои производственные возможности, то в модели задачи необходимо изменить
-: только целевую функцию
+: целевую функцию и систему ограничений
-: только систему ограничений
Источник
ÐÑедположим Ð´Ð»Ñ Ð¾Ð¿ÑеделенноÑÑи, ÑÑо Ð½ÐµÐ¾Ð±Ñ Ð¾Ð´Ð¸Ð¼Ð¾ ÑоÑÑавиÑÑ ÑамÑй деÑевÑй ÑаÑион пиÑÐ°Ð½Ð¸Ñ ÑÑплÑÑ, ÑодеÑжаÑий Ð½ÐµÐ¾Ð±Ñ Ð¾Ð´Ð¸Ð¼Ð¾Ðµ колиÑеÑÑво опÑеделеннÑÑ Ð¿Ð¸ÑаÑелÑнÑÑ Ð²ÐµÑеÑÑв (Ð´Ð»Ñ Ð¿ÑоÑÑоÑÑ, Ñиамина Т и ниаÑина Ð).
ТаблиÑа 8.1
ÐÑÑ Ð¾Ð´Ð½Ñе даннÑе в задаÑе об опÑимизаÑии ÑмеÑи
СодеÑжание в 1 ÑнÑии Ð | СодеÑжание в 1 ÑнÑии С | ÐоÑÑебноÑÑÑ | |
ÐеÑеÑÑво Т | 0,10 мг | 0,25 мг | 1,00 мг |
ÐеÑеÑÑво Ð | 1,00 мг | 0,25 мг | 5,00 мг |
ÐалоÑии | 110,00 | 120,00 | 400,00 |
СÑоимоÑÑÑ 1 ÑнÑии, в ÑенÑÐ°Ñ | 3,8 | 4,2 |
ÐиÑÐµÐ²Ð°Ñ ÑенноÑÑÑ ÑаÑиона (в калоÑиÑÑ ) должна бÑÑÑ Ð½Ðµ менее заданной. ÐÑÑÑÑ Ð´Ð»Ñ Ð¿ÑоÑÑоÑÑ ÑмеÑÑ Ð´Ð»Ñ ÑÑплÑÑ Ð¸Ð·Ð³Ð¾ÑавливаеÑÑÑ Ð¸Ð· двÑÑ Ð¿ÑодÑкÑов – Ри С. ÐзвеÑÑно ÑодеÑжание Ñиамина и ниаÑина в ÑÑÐ¸Ñ Ð¿ÑодÑкÑÐ°Ñ , а Ñакже пиÑаÑелÑÐ½Ð°Ñ ÑенноÑÑÑ Ð Ð¸ С (в калоÑиÑÑ ). СколÑко Ри С надо взÑÑÑ Ð´Ð»Ñ Ð¾Ð´Ð½Ð¾Ð¹ поÑÑии кÑÑиного коÑма, ÑÑÐ¾Ð±Ñ ÑÑплÑÑа полÑÑили Ð½ÐµÐ¾Ð±Ñ Ð¾Ð´Ð¸Ð¼ÑÑ Ð¸Ð¼ Ð´Ð¾Ð·Ñ Ð²ÐµÑеÑÑв Ри Т и калоÑий (или болÑÑе), а ÑÑоимоÑÑÑ Ð¿Ð¾ÑÑии бÑла минималÑна? ÐÑÑ Ð¾Ð´Ð½Ñе даннÑе Ð´Ð»Ñ ÑаÑÑеÑов пÑÐ¸Ð²ÐµÐ´ÐµÐ½Ñ Ð² Табл. 8.1.
ÐадаÑа линейного пÑогÑаммиÑÐ¾Ð²Ð°Ð½Ð¸Ñ Ð¸Ð¼ÐµÐµÑ Ð²Ð¸Ð´:
3,8K+4,2Cð min
0,10K+0,25C≥1,00
1,00K+0,25C≥5,00
110K+120C≥400,00
K≥0
C≥0
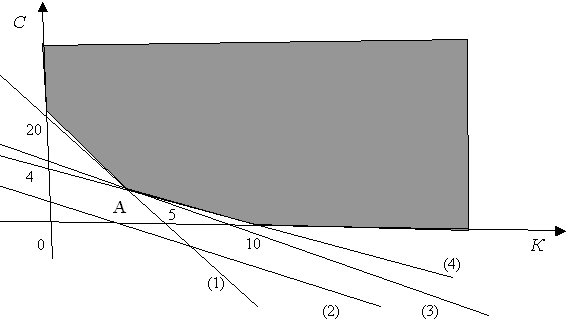
Ðе гÑаÑиÑеÑкое ÑеÑение пÑедÑÑавлено на РиÑ. 8.1

РиÑ. 8.41. ÐÑаÑиÑеÑкое ÑеÑение задаÑи об опÑимизаÑии ÑмеÑи
Ðа ÑиÑ. 8.4 Ñади облегÑÐµÐ½Ð¸Ñ Ð²Ð¾ÑпÑиÑÑÐ¸Ñ ÑеÑÑÑе пÑÑмÑе обознаÑÐµÐ½Ñ Ð½Ð¾Ð¼ÐµÑами (1) – (4). ÐÑÑÐ¼Ð°Ñ (1) опиÑÑваеÑÑÑ ÑÑавнением 1,00K+0,25C=5,00 (огÑаниÑение по веÑеÑÑÐ²Ñ Ð). Ðна пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ, как и показано на ÑиÑÑнке, ÑеÑез ÑоÑки (5, 0) на оÑи абÑÑиÑÑ Ð¸ (0, 20) на оÑи оÑдинаÑ. ÐбÑаÑиÑе внимание, ÑÑо допÑÑÑимÑе знаÑÐµÐ½Ð¸Ñ Ð¿Ð°ÑамеÑÑов (Ð, С) Ð»ÐµÐ¶Ð°Ñ Ð²ÑÑе пÑÑмой (1) или на ней, в оÑлиÑие Ð¾Ñ Ñанее ÑаÑÑмоÑÑеннÑÑ ÑлÑÑаев в пÑедÑдÑÑей пÑоизводÑÑвенной задаÑе линейного пÑогÑаммиÑованиÑ.
ÐÑÑÐ¼Ð°Ñ (2) – ÑÑо пÑÑÐ¼Ð°Ñ 110K+120C=400,00 (огÑаниÑение по калоÑиÑм). ÐбÑаÑим внимание, ÑÑо в облаÑÑи неоÑÑиÑаÑелÑнÑÑ Ð¡ она ÑаÑположена вÑÑÐ´Ñ Ð½Ð¸Ð¶Ðµ пÑÑмой (1). ÐейÑÑвиÑелÑно, ÑÑо веÑно пÑи K=0, пÑÑÐ¼Ð°Ñ (1) пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ ÑеÑез ÑоÑÐºÑ (0, 20), а пÑÑÐ¼Ð°Ñ (2) – ÑеÑез ÑаÑположеннÑÑ Ð½Ð¸Ð¶Ðµ ÑоÑÐºÑ (0, 400/120). ТоÑка пеÑеÑеÑÐµÐ½Ð¸Ñ Ð´Ð²ÑÑ Ð¿ÑÑмÑÑ Ð½Ð°Ñ Ð¾Ð´Ð¸ÑÑÑ Ð¿Ñи ÑеÑении ÑиÑÑÐµÐ¼Ñ ÑÑавнений
1,00K+0,25C=5,00
110K+120C=400,00
Ðз пеÑвого ÑÑÐ°Ð²Ð½ÐµÐ½Ð¸Ñ K=5-0,25C. ÐодÑÑавим во вÑоÑое:
110(5-0,25C)+120C=400, оÑкÑда 550-27,5C+120C=400. СледоваÑелÑно, 150=-92,5C , Ñ. е. ÑеÑение доÑÑигаеÑÑÑ Ð¿Ñи оÑÑиÑаÑелÑном С. ÐÑо и ознаÑаеÑ, ÑÑо пÑи вÑеÑ
положиÑелÑнÑÑ
С пÑÑÐ¼Ð°Ñ (2) Ð»ÐµÐ¶Ð¸Ñ Ð½Ð¸Ð¶Ðµ пÑÑмой (1). ÐнаÑиÑ, еÑли вÑполнено огÑаниÑение по Ð, Ñо обÑзаÑелÑно вÑполнено и огÑаниÑение по калоÑиÑм. ÐÑ ÑÑолкнÑлиÑÑ Ñ Ð½Ð¾Ð²Ñм Ñвлением – некоÑоÑÑе огÑаниÑÐµÐ½Ð¸Ñ Ñ Ð¼Ð°ÑемаÑиÑеÑкой ÑоÑки зÑÐµÐ½Ð¸Ñ Ð¼Ð¾Ð³ÑÑ Ð¾ÐºÐ°Ð·Ð°ÑÑÑÑ Ð»Ð¸Ñними. С ÑкономиÑеÑкой ÑоÑки зÑÐµÐ½Ð¸Ñ Ð¾Ð½Ð¸ необÑ
одимÑ, оÑÑажаÑÑ ÑÑÑеÑÑвеннÑе ÑеÑÑÑ Ð¿Ð¾ÑÑановки задаÑи, но в данном ÑлÑÑае внÑÑÑеннÑÑ ÑÑÑÑкÑÑÑа задаÑи оказалаÑÑ Ñакова, ÑÑо огÑаниÑение по калоÑиÑм не ÑÑаÑÑвÑÐµÑ Ð² ÑоÑмиÑовании допÑÑÑимой облаÑÑи паÑамеÑÑов и наÑ
ождении ÑеÑениÑ.
ÐÑÑÐ¼Ð°Ñ (4) – ÑÑо пÑÑÐ¼Ð°Ñ 0,1K+0,25C=1 (огÑаниÑение по веÑеÑÑÐ²Ñ Ð¢). Ðна пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ, как и показано на ÑиÑÑнке, ÑеÑез ÑоÑки (10, 0) на оÑи абÑÑиÑÑ Ð¸ (0, 4) на оÑи оÑдинаÑ. ÐбÑаÑиÑе внимание, ÑÑо допÑÑÑимÑе знаÑÐµÐ½Ð¸Ñ Ð¿Ð°ÑамеÑÑов (Ð, С) Ð»ÐµÐ¶Ð°Ñ Ð²ÑÑе пÑÑмой (4) или на ней, как и Ð´Ð»Ñ Ð¿ÑÑмой (1).
СледоваÑелÑно, облаÑÑÑ Ð´Ð¾Ð¿ÑÑÑимÑÑ Ð·Ð½Ð°Ñений паÑамеÑÑов (Ð, С) ÑвлÑеÑÑÑ Ð½ÐµÐ¾Ð³ÑаниÑенной ÑвеÑÑ Ñ. Ðз вÑей плоÑкоÑÑи она вÑделÑеÑÑÑ Ð¾ÑÑми кооÑÐ´Ð¸Ð½Ð°Ñ (Ð»ÐµÐ¶Ð¸Ñ Ð² пеÑвом квадÑанÑе) и пÑÑмÑми (1) и (4) (Ð»ÐµÐ¶Ð¸Ñ Ð²ÑÑе ÑÑÐ¸Ñ Ð¿ÑÑмÑÑ , а Ñакже вклÑÑÐ°ÐµÑ Ð³ÑаниÑнÑе оÑÑезки). ÐблаÑÑÑ Ð´Ð¾Ð¿ÑÑÑимÑÑ Ð·Ð½Ð°Ñений паÑамеÑÑов, Ñ. е. ÑоÑек (Ð, С), можно назваÑÑ “неогÑаниÑеннÑм многоÑголÑником”. ÐинимÑм Ñелевой ÑÑнкÑии 3.8K+4,2C Ð¼Ð¾Ð¶ÐµÑ Ð´Ð¾ÑÑигаÑÑÑÑ ÑолÑко в веÑÑÐ¸Ð½Ð°Ñ ÑÑого “многоÑголÑника”. ÐеÑÑин вÑего ÑÑи. ÐÑо пеÑеÑеÑÐµÐ½Ð¸Ñ Ñ Ð¾ÑÑми абÑÑиÑÑ (10, 0) и оÑÐ´Ð¸Ð½Ð°Ñ (0, 20) пÑÑмÑÑ (1) и (4) (в каждом ÑлÑÑае из двÑÑ Ð¿ÐµÑеÑеÑений беÑеÑÑÑ Ñо, коÑоÑое ÑдовлеÑвоÑÑÐµÑ Ð¾Ð±Ð¾Ð¸Ð¼ огÑаниÑениÑм). ТÑеÑÑÑ Ð²ÐµÑÑина – ÑÑо ÑоÑка РпеÑеÑеÑÐµÐ½Ð¸Ñ Ð¿ÑÑмÑÑ (1) и (4), кооÑдинаÑÑ ÐºÐ¾ÑоÑой Ð½Ð°Ñ Ð¾Ð´ÑÑÑÑ Ð¿Ñи ÑеÑении ÑиÑÑÐµÐ¼Ñ ÑÑавнений
0,10K+0,25C=1,00
1,00K+0,25C=5,00
Ðз вÑоÑого ÑÑÐ°Ð²Ð½ÐµÐ½Ð¸Ñ K=5-0,25C, из пеÑвого
0,1(5-0,25C)+0,25C=5,00=0,25C=0,5+0,225C=1, оÑкÑда C=0,5/0,225=20/9 и K=5-5/9=40/9. ÐÑак, A=(20/9,40/9).
ÐÑÑÐ¼Ð°Ñ (3) на РиÑ. 8.5 – ÑÑо пÑÑмаÑ, ÑооÑвеÑÑÑвÑÑÑÐ°Ñ Ñелевой ÑÑнкÑии 3,8K+4,2C. Ðна пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ Ð¼ÐµÐ¶Ð´Ñ Ð¿ÑÑмÑми (1) и (4), задаÑÑими огÑаниÑениÑ, и минимÑм доÑÑигаеÑÑÑ Ð² ÑоÑке Ð, ÑеÑез коÑоÑÑÑ Ð¸ пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ Ð¿ÑÑÐ¼Ð°Ñ (3). СледоваÑелÑно, минимÑм Ñавен 3,8X40/9+4,2X20/9=236/9. ÐадаÑа об опÑимизаÑии ÑмеÑи полноÑÑÑÑ ÑеÑена.
ÐвойÑÑÐ²ÐµÐ½Ð½Ð°Ñ Ð·Ð°Ð´Ð°Ñа, поÑÑÑÐ¾ÐµÐ½Ð½Ð°Ñ Ð¿Ð¾ Ñанее опиÑаннÑм пÑавилам, Ð¸Ð¼ÐµÐµÑ Ð¿ÑиведеннÑй ниже вид (Ð¼Ñ Ð¿Ð¾Ð²ÑоÑÑем здеÑÑ Ð¸ иÑÑ Ð¾Ð´Ð½ÑÑ Ð·Ð°Ð´Ð°ÑÑ Ð¾Ð± опÑимизаÑии ÑмеÑи, ÑÑÐ¾Ð±Ñ Ð½Ð°Ð³Ð»Ñдно пÑодемонÑÑÑиÑоваÑÑ ÑÐµÑ Ð½Ð¾Ð»Ð¾Ð³Ð¸Ñ Ð¿Ð¾ÑÑÑÐ¾ÐµÐ½Ð¸Ñ Ð´Ð²Ð¾Ð¹ÑÑвенной задаÑи):
3,8K+4,2Cð min W1+5W2+400W3ð max
0,10K+0,25C ≥1,00 0,1W1+1,10W2+110W3≤3,8
1,00K+0,25C ≥5,00 0,25W1+0,25W2+120W3≤4,2
110K+120C ≥400,00 W1≥0
K ≥0 W2≥0
C ≥0 W3≥0
ÐинималÑное знаÑение в пÑÑмой задаÑе, как и должно бÑÑÑ, Ñавно макÑималÑÐ½Ð¾Ð¼Ñ Ð·Ð½Ð°ÑÐµÐ½Ð¸Ñ Ð² двойÑÑвенной задаÑе, Ñ. е. оба ÑиÑла ÑÐ°Ð²Ð½Ñ 236/9. ÐнÑеÑпÑеÑаÑÐ¸Ñ Ð´Ð²Ð¾Ð¹ÑÑвеннÑÑ Ð¿ÐµÑеменнÑÑ : W1 – “ÑÑоимоÑÑÑ” единиÑÑ Ð²ÐµÑеÑÑва Т, а W2 – “ÑÑоимоÑÑÑ” единиÑÑ Ð²ÐµÑеÑÑва Ð, измеÑеннÑе “по Ð¸Ñ Ð²ÐºÐ»Ð°Ð´Ñ” в ÑелевÑÑ ÑÑнкÑиÑ. ÐÑи ÑÑом W3=0, поÑколÑÐºÑ Ð¾Ð³ÑаниÑение на ÑиÑло калоÑий никак не ÑÑаÑÑвÑÐµÑ Ð² ÑоÑмиÑовании опÑималÑного ÑеÑениÑ. ÐÑак, W1,W2,W3 – ÑÑо Ñ. н. обÑекÑивно обÑÑловленнÑе оÑенки (по Ð. Ð. ÐанÑоÑовиÑÑ) ÑеÑÑÑÑов (веÑеÑÑв Т и Ð, калоÑий).
Источник
