Решение задач о диете в линейном программировании пример решения
В поисках оптимальной диеты методом линейного программирования -2
Разработка под Windows, Математика, Python

Вопрос диеты всегда будоражил умы слабого пола и не только. Не взирая на большое количество рекомендаций диетологов, вопрос диеты для многих так и остаётся нерешённым. В таких условиях хочу предложить альтернативный вариант, особо не привлекая диетологию, а опираясь исключительно на линейное программирование, надеюсь, неплохой повод уже серьёзно задуматься о проблеме.
Должна ли диета быть экономной?
Для поддержания нормальной жизнедеятельности человеку необходимо потреблять в день не менее 118 г белков, 56 г жиров, 500 г углеводов и 28 г минеральных солей. Эти питательные вещества содержатся в разных количествах и разных пищевых продуктах.
В таблице приведено количество питательных веществ в различных продуктах в г/кг и цена этих продуктов за 1 кг. Необходимо составить дневной рацион, содержащий минимальную суточную норму питательных веществ при минимальной их стоимости.
Обозначив через: Х1 –количество мяса; Х2- количество рыбы; Х3- количество молока; Х4- количество масла; Х5- количество сыра; Х6- количество крупы; Х7- количество картофеля, потребляемых человеком в день. Можем составить уравнение общей стоимости F питания в день:
F=333*X1+308*X2+52*X3+400*X4+450*X5+56*X6+25*X7
Нам нужно найти минимум F.
Суммарное количество белков в рационе человека должно быть не меньше 118 г. Отсюда,
180*X1+190*X2+30*X3+10*X4+260*X5+130*X6+21*X7?118
Такие же неравенства составляем для жиров, углеводов и солей. Имеем:
20*X1+3*X2+40*X3+865*X4+310*X5+30*X6+2*X7?56
50*X3+6*X4+20*X5+650*X6+200*X7?500
9*X1+10*X2+7*X3+12*X4+60*X5+20*X6+10*X7?28
Решим задачу на Python
from cvxopt.modeling import variable, op
import time
start = time.time()
x = variable(7, ‘x’)
z=(333*x[0] + 308*x[1] +52* x[2] +400*x[3] +450*x[4] +56* x[5]+20*x[6])
mass1 =(- (180*x[0] + 190*x[1] +30* x[2] +10*x[3] +260*x[4] +130* x[5]+21*x[6]) <= -118)
mass2 =(- (20*x[0] + 3*x[1] +40* x[2] +865*x[3] +310*x[4] +30* x[5]+2*x[6]) <= -56)
mass3 =(- (50* x[2] +6*x[3] +20*x[4] +650* x[5]+200*x[6]) <= -500)
mass4 =(- (9*x[0] + 10*x[1] +7* x[2] +12*x[3] +60*x[4] +20* x[5]+10*x[6]) <= -28)
x_non_negative = (x >= 0)
problem =op(z,[mass1,mass2,mass3,mass4 ,x_non_negative])
problem.solve(solver=’glpk’)
problem.status
print(“Результат:”)
print(round(1000*x.value[0],1),’-грамм мяса, затраты -‘,round(x.value[0]*333,1),’руб.’)
print(round(1000*x.value[1],1),’-грамм рыбы, затраты -‘,round(x.value[1]*308,1),’руб.’)
print(round(1000*x.value[2],1),’-миллилитров молока, затраты -‘,round(x.value[2]*52,1),’руб.’)
print(round(1000*x.value[3],1),’-грамм масла, затраты -‘,round(x.value[3]*400,1),’руб.’)
print(round(1000*x.value[4],1),’-грамм сыр, затраты -‘,round(x.value[4]*450,1),’руб.’)
print(round(1000*x.value[5],1),’-грамм крупы, затраты -‘,round(x.value[5]*56,1),’руб.’)
print(round(1000*x.value[6],1),’-грамм картофеля, затраты -‘,round(x.value[6]*25,1),’руб.’)
print(round(problem.objective.value()[0],1),”- стоимость рациона одного человека в день”)
stop = time.time()
print (“Время :”,round(stop-start,3))
Следует отметить некоторые особенности написания программы с использованием модуля cvxopt. Modeling: все переменные сохраняются в списках, а индексы списков начинаются не с 1, а с ; в условиях, которые записываются в виде нестрогих неравенств должно быть установлено ограничение сверху, поэтому, для перехода от ограничения снизу, обе части неравенств умножены на -1.
Результат:
0.0 -грамм мяса, затраты — 0.0 руб.
0.0 -грамм рыбы, затраты — 0.0 руб.
0.0 -миллилитров молока, затраты — 0.0 руб.
38.0 -грамм масла, затраты — 15.2 руб.
-0.0 -грамм сыр, затраты — -0.0 руб.
679.3 -грамм крупы, затраты — 38.0 руб.
1395.9 -грамм картофеля, затраты — 34.9 руб.
81.1 — стоимость рациона одного человека в день
Время: 0.09
Анализ результатов показывает: ни мяса, ни рыбы- крупа, масло и картофель — вот такое линейное программирование. Вряд ли такой рацион можно рассматривать серьёзно, но для общности анализа пусть будет. А мы продолжим поиск.
Должна ли диета быть калорийной?
Для определённости предположим, что в качестве исходных продуктов рассмотрим хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград – всего семь продуктов. В качестве питательных веществ – белки, жира, углеводы.
Калорийность одной весовой единицы каждого из продуктов следующая: c1=2060, c2=2430, c3=3600, c4=890, c5=140, c6=230, c7=650.
Содержание питательных веществ в продуктах питания поместим в следующую таблицу.
Минимальная суточная потребность человека в питательных веществах следующая: в белках b1=100, в жирах b2=70, в углеводах b3=400.
Не уменьшая общности решаемой задачи, можно считать, что калорийность продуктов измеряется в килокалориях/кг, суточная потребность в питательных веществах – в граммах, а содержание питательных веществ в продуктах– в граммах/кг. В указанных условиях становится возможным выполнить дополнительную проверку сформированных условий задачи на основе рассмотрения физической размерности целевой функции и ограничений.
Обозначив через: x1 –количество хлеба; x2- количество мяса; x3- количество сыра; x4- количество бананов; x5- количество огурцов; x6- количество помидоров; x7- количество винограда, потребляемых человеком в день в килограммах.
Можем составить уравнение общей калорийности F питания в день:
F=2060*x1 + 2430*x2 +3600* x3+890*x4 +140*x5 +230* x6+650*x7
Нам нужно найти минимум F.
Суммарное количество белков в рационе человека должно быть не меньше 100 г. Отсюда
61*x1+ 220*x2 +230* x3 +15*x4 +8*x5 +11* x6+6*x7 ?100
Такие же неравенства составляем для жиров и углеводов. Имеем:
12*x1 +172*x2 +290* x3+1*x4 +1*x5 +2* x6+2*x7 ?70
420*x1 +0*x2 +0* x3 +212*x4+26*x5 +38* x6+155*x7 ?400
Решим задачу на Python
from cvxopt.modeling import variable, op
import time
start = time.time()
x = variable(7, ‘x’)
z=(333*x[0] + 308*x[1] +52* x[2] +400*x[3] +450*x[4] +56* x[5]+20*x[6])
mass1 =(- (180*x[0] + 190*x[1] +30* x[2] +10*x[3] +260*x[4] +130* x[5]+21*x[6]) <= -118)
mass2 =(- (20*x[0] + 3*x[1] +40* x[2] +865*x[3] +310*x[4] +30* x[5]+2*x[6]) <= -56)
mass3 =(- (50* x[2] +6*x[3] +20*x[4] +650* x[5]+200*x[6]) <= -500)
mass4 =(- (9*x[0] + 10*x[1] +7* x[2] +12*x[3] +60*x[4] +20* x[5]+10*x[6]) <= -28)
x_non_negative = (x >= 0)
problem =op(z,[mass1,mass2,mass3,mass4 ,x_non_negative])
problem.solve(solver=’glpk’)
problem.status
print(“Результат:”)
print(round(1000*x.value[0],1),’-грамм хлеба’)
print(round(1000*x.value[1],1),’-грамм мяса’)
print(round(1000*x.value[2],1),’-грамм сыра’)
print(round(1000*x.value[3],1),’-грамм бананов’)
print(round(1000*x.value[4],1),’-грамм огурцов’)
print(round(1000*x.value[5],1),’-грамм помидоров’)
print(round(1000*x.value[6],1),’-грамм винограда’)
print(round(problem.objective.value()[0],1),”-Калорийность рациона одного человека в день”)
stop = time.time()
print (“Время :”,round(stop-start,3))
Результат:
0.0 -грамм хлеба
211.5 -грамм мяса
109.4 -грамм сыра
1886.8 -грамм бананов
0.0 -грамм огурцов
0.0 -грамм помидоров
0.0 -грамм винограда
2587.1 -килокалорий -калорийность
рациона одного человека в день
Время: 0.06
Анализ результатов решения показывает, что для удовлетворения суточной потребности в питательных веществах (белки, жиры, углеводы), следует использовать 211 грамм мяса баранины, 109 грамм сыра, 1887 грамм бананов, совсем отказаться от хлеба, огурцов, помидоров и винограда. При этом общая калорийность найденной оптимальной диеты будет равна 2587 килокалорий, что вполне соответствует малоактивному образу жизни без существенных физических нагрузок. Напомним, что согласно медицинским данным, энергетические затраты работников умственного труда (программисты, юристы, врачи, педагоги, бухгалтера) лежат в пределах 3000 килокалорий.
Содержательный анализ результатов задачи об оптимальной диете явно выявляет недостатки рассмотренной математической модели. С одной стороны, для вкусной и питательной пищи не всегда приемлемым оказывается ограниченный рацион продуктов питания, который совершенно игнорирует индивидуальные предпочтения при выборе отдельных продуктов. С другой стороны, найденное оптимальное решение (мясо + сыр + бананы) для многих покажется однообразным и способным повергнуть в уныние даже пациентов больницы. Наконец, рассмотренная математическая модель задачи об оптимальной диете не учитывает суточную потребность в витаминах и микроэлементах, учет которых может существенно повлиять на выбор оптимального состава продуктов.
Что можно предложить заинтересованному читателю?
Заинтересованным читателям данной публикации в качестве упражнения предлагается рассмотреть собственную постановку задачи об оптимальной диете, отражающую их индивидуальные предпочтения в выборе тех или иных продуктов. При этом условия задачи можно несколько изменить, включив в качестве одного из ограничений общую калорийность диеты, а в качестве целевой функции рассмотреть общую массу наиболее предпочтительных продуктов.
Решение задачи на Python (только как пример)
from cvxopt.modeling import variable, op
import time
start = time.time()
x = variable(7, ‘x’)
z=( x[0] + x[1] +x[2] +x[3] +x[4] +x[5]+x[6])
mass1 =(- (61*x[0] + 220*x[1] +230* x[2] +15*x[3] +8*x[4] +11* x[5]+6*x[6]) <= -100)
mass2 =(- (12*x[0] +172*x[1] +290* x[2] +1*x[3] +1*x[4] +2* x[5]+2*x[6]) <= -70)
mass3 =(- (420*x[0] +0*x[1] +0* x[2] +212*x[3] +26*x[4] +38* x[5]+155*x[6]) <= -400)
mass4 =(-( 2060*x[0] + 2430*x[1] +3600* x[2] +890*x[3] +140*x[4] +230* x[5]+650*x[6]) <= -3000)
x_non_negative = (x >= 0)
problem =op(z,[mass1,mass2,mass3, mass4,x_non_negative])
problem.solve(solver=’glpk’)
problem.status
print(“Результат:”)
print(round(1000*x.value[0],1),’-грамм хлеба’)
print(round(1000*x.value[1],1),’-грамм мяса’)
print(round(1000*x.value[2],1),’-грамм сыра’)
print(round(1000*x.value[3],1),’-грамм бананов’)
print(round(1000*x.value[4],1),’-грамм огурцов’)
print(round(1000*x.value[5],1),’-грамм помидоров’)
print(round(1000*x.value[6],1),’-грамм винограда’)
print(round(problem.objective.value()[0],1),”-килограмм-общая масса продуктов из n рациона одного человека в день”)
stop = time.time()
print (“Время :”,round(stop-start,3))
Результат:
952.4 -грамм хлеба
0.0 -грамм мяса
288.4 -грамм сыра
0.0 -грамм бананов
0.0 -грамм огурцов
0.0 -грамм помидоров
0.0 -грамм винограда
1.2 -килограмм-общая масса продуктов из
рациона одного человека в день
Время: 0.051
Это мне напоминает рацион долгожителей высокогорных районов лепёшки на козьем молоке и сыр того же происхождения, но воспоминания скорее всего обманчивы, поскольку список продуктов явно не оттуда.
Вместо вывода
Несмотря на выявленные недостатки рассмотренной математической модели задачи об оптимальной диете, найденное оптимальное решение в точности соответствует исходной постановке задачи. Это свидетельствует о достаточно высокой точности решения задач линейного программирования при помощи библиотеки cvxopt. Modeling Python.
Интерфейс программы настолько простой и наглядный, что не требует каких-либо дополнительных навыков. Достаточно скачать и установить последнюю версию Python, например, с сайта [1], а библиотеку cvxopt с сайта [2]. Затем создать файл с расширением py и поместить в него любую из приведенных в статье программ, предварительно модифицировав её под свою задачу с новой функцией цели и ограничениями.
Ссылки
- Python.
- Windows binaries for python.
Источник
На главную страницу
Линейное
программирование
В конец страницы
10.1. ПРИМЕРЫ ЗАДАЧ
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
1. Задача использования сырья
(задача планирования производства).
Для изготовления двух видов
продукции и
используют
три вида сырья: ,
и
.
Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы
продукции, а также величина прибыли, получаемая от реализации единицы продукции,
приведены в таблице 10.1. Необходимо составить такой план выпуска продукции,
чтобы при ее реализации получить максимальную прибыль.
Таблица 10.1
Виды сырья | Запасы сырья | Количество единиц | |
Прибыль от единицы (в руб.) | |||
Составим
экономико-математическую модель (математическое описание исследуемого
экономического процесса) задачи.
Обозначим через
,
количество
единиц продукции соответственно ,
,
запланированных к производству. Тогда учитывая количество единиц сырья,
затрачиваемых на изготовление единицы продукции, а также запасы сырья, получим
систему ограничений
(10.1)
По смыслу задачи переменные
,
.
(10.2)
Суммарная прибыль
F(x) составит
руб.
от реализации продукции и
руб.
– от реализации продукции ,
т.е.
.
(10.3)
Итак, экономико-математическая
модель задачи: найти такой план выпуска продукции
,
удовлетворяющий системе (10.1) и условию (10.2), при котором функция (10.3)
принимает максимальное значение.
Задачу легко обобщить на случай
выпуска n видов продукции с использованием
m видов сырья.
2. Задача составления рациона
(задача о диете).
Имеется два вида корма
I и II, содержащие
питательные вещества (витамины) ,
и
.
Содержание количества единиц питательного вещества в 1 кг каждого вида корма и
стоимость 1 кг корма приведены в таблице 10.2.
Таблица
10.2
Питательные вещества | Необходимый минимум | Количество единиц | |
Корм | Корм | ||
Стоимость 1 кг корма | |||
Необходимо составить дневной
рацион, в котором содержание каждого вида питательных веществ было бы не менее
установленного минимума, причем затраты на него должны быть минимальными.
Составим экономико-математическую
модель задачи. Обозначим через и
соответственно
количество кормов I и II,
входящих в дневной рацион. Принимая во внимание значения, приведенные в табл.
10.2, и условие, что дневной рацион удовлетворяет требуемой питательности только
в случае, если количество единиц питательных веществ не меньше предусмотренного,
получим систему ограничений
(10.4)
Кроме того, переменные
,
. (10.5)
Общая стоимость рациона (в руб.)
составит
. (10.6)
Итак, экономико-математическая
модель задачи: составить дневной рацион
,
удовлетворяющий системе (10.4) и условию (10.5), при котором функция (10.6)
принимает минимальное значение.
3. Задача о раскрое материалов.
На раскрой поступает материал
одного образца в количестве a единиц. Требуется
изготовить из него l разных комплектующих
изделий в количествах пропорциональных числам
,
,
…, (условие
комплектности). Каждая единица материала может быть раскроена
n различными способами, при этом использование
i-го способа (i
=1, 2, …, n) дает
единиц
k-го изделия (k
= 1, 2, …, l). Требуется составить план
раскроя, обеспечивающий максимальное количество комплектов.
Составим экономико-математическая
модель задачи. Обозначим через количество
единиц материала, раскраиваемых i-м способом, и
x – количество изготавливаемых комплектов
изделий.
Так как общее количество материала
равно сумме его единиц, раскраиваемых различными способами, то
(10.7)
Условие комплектности выразится
уравнениями
(k
= 1, 2, …, l)
(10.8)
по смыслу задачи переменные
(i
= 1, 2, …, n).
(10.9)
Итак, экономико-математическая
модель задачи: найти такое решение ,
удовлетворяющее системе уравнений (10.7) – (10.8) и условию (10.9), при котором
функция F = x
принимает максимальное значение.
Назад К
началу страницы
Вперед
Источник
2.1. Задача о диете
Исторические задача о диете является одной из первых задач линейного
программирования.
Постановка задачи – первый и наиболее важный этап построения модели,
способный обеспечить правильное решение проблемы.
Даме необходимо похудеть, за помощью обратилась к подруге.
Построение модели – рассмотрение этого этапа и является главной целью.
Подруга посоветовала перейти на рациональное питание, состоящее из двух
продуктов P и Q.
Суточное питание этими продуктами должно давать не более 14 единиц жира
(чтобы похудеть), но не менее 300 калорий. На упаковке продукта Р
написано, что в одном килограмме этого продукта содержится 15 единиц жира и 150
калорий, а на упаковке с продуктом Q – 4
единицы жира и 200 калорий соответственно. При этом цена 1 килограмма продукта
Р равна 15 руб., а 1 кг продукта Q – 25
руб.
Так как дама была стеснена в средствах, но ее интересовал вопрос: в какой
пропорции нужно брать эти продукты для того, чтобы выдержать условия диеты и
истратить как можно меньше денег?
Перейдем к формализации данной ситуации на языке математических символов.
Обозначим через х количество продукта Р и
через у количество продукта Q, требуемые
для выполнения условий диеты.
Количество единиц жира, содержащегося в х кг продукта
Р и в у кг продукта Q, равно
15х + 4 и по условию диеты не должно превосходить 14:
В свою очередь, количество калорий, содержащихся в х
кг продукта Р и в у кг продукта Q,
равно 150х + 200у и по условию диеты должно быть не меньше 300:
Теперь о стоимости z продуктов.
Она равна
и в соответствии с высказанными пожеланиями должна быть минимальной.
Последнее записывается так:
Тем самым мы получили систему формул:
которую решим графическим способом.
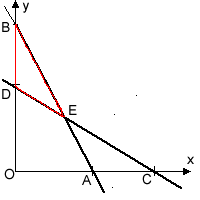
Нас интересует только та ее часть, которая лежит над треугольником
BDE. Вычисляя значения z
во всех трех вершинах этого треугольника
и сравнивая полученные результаты, замечаем, что наименьшее значение (35)
достигается в вершине Е. Таким образом,
и искомая пропорция – 2 : 3.
2.2. Задача о выпуске продукции
Фирма выпускает два вида древесно-стружечных плит – обычные и
улучшенные. При этом производится две основные операции – прессование и отделка.
Требуется указать, какое количество плит каждого типа можно изготовить в течение
месяца так, чтобы обеспечить максимальную прибыль при следующих ограничениях на
ресурсы (материал, время, затраты):
Затраты | Партия из 100 плит | Имеющиеся ресурсы на месяц | |
обычных | улучшенных | ||
| Материал (фунты) Время на прессование (часы) Время на отделку (часы) Средства (деньги) | 20 | 40 | 4000 |
| Прибыль | 80 | 100 | max |
Перейдем к построению математической модели
поставленной задачи. Введем следующие обозначения. Пусть
х – количество партий в 100 плит обычного
вида, изготавливаемых в течение месяца;
у – количество партий в 100 плит
улучшенного качества, изготавливаемых в течение месяца.
Тогда ожидаемую прибыль можно записать так:
Требуется найти такие значения х и у,
подчиненные условиям
для которых
Для того, чтобы найти в первой четверти плоскости хОу
множество точек, координаты (х, у) которых удовлетворяют указанным выше
неравенствам, необходимо сначала построить прямые (по точкам их пересечения с
координатными осями)
а затем, используя точку начала отсчета О(0, 0),
определить соответствующие полуплоскости. Пересечением полученных полуплоскостей
будет четырехугольник ОВМЕ.
Наша целевая функция достигает наибольшего значения в одной
из вершин четырехугольника.
Нам необходимо найти координаты точки М – точки
пересечения прямых EF и АВ, для этого надо
решить систему уравнений
Вычислить значения z в точках
В(0, 100), Е(150, 0), М(100, 50):
Из полученных значений выберем наибольшее и получим ответ:
2.3. Общая задача линейного программирования
В общем случае и число неизвестных , и число ограничений
могут достигать десятков, сотен, тысяч и т.д. Однако набор соответствующих
условий ничем (кроме количества) от рассмотренных выше примеров не отличается.
Это нетрудно заметить уже по общей постановке задачи линейного программирования.
Стандартная математическая формулировка общей задачи
линейного программирования выглядит так: требуется найти экстремальное значение
показателя эффективности (целевой функции)
(линейной функции элементов решения
) при линейных ограничительных
условиях, накладываемых на элементы решения:
где – заданные числа.
Что касается существующих методов решения этой задачи с
числом переменных, больших двух, то в их основе лежат те же идеи, на которые мы
опирались при разработке графического подхода. Конечно, в случае сильного
увеличения числа переменных и ограничений техника получения решения заметно
усложняется, но она опирается на совершенно стандартные, хорошо разработанные
алгоритмы (возникающие трудности связаны лишь с ростом объема необходимых
вычислений).
Общую постановку задачи линейного программирования можно
записать в более компактной форме, если воспользоваться следующим правилом.
Правило сокращенного суммирования. Для обозначения
суммы чисел :
принята такая запись:
где ∑ – знак суммирования, а
k – индекс суммирования.
Это обозначение очень удобно:
А вот как выглядит запись общей задачи линейного
программирования:
2.4. Транспортная задача
Важный тип задач линейного программирования представляет
задача о перевозках. Называется она так потому, что цель этой задачи
заключается в минимизации полной стоимости перевозок известного количества
товаров со складов к потребителю.
Сбалансированная задача – задача о перевозках, в
которой общий объем товаров, готовых к отправлению, в точности равен объему
товаров, который готовы принять в пунктах назначения.
Пример 1. Рассмотрим транспортную задачу, заданную таблицей
| В | Наличие | |||
| 1 | 2 | |||
| А | 1 2 | 1 2 | 2 1 | 20 10 |
| Запрос | 16 | 14 | 30 | |
Решение. Пусть – искомое число единиц
товара, пересылаемого из пункта в пункт
. Тогда данные таблицы можно
представить в следующем виде:
при условии, что
Положим и выразим через
t остальные переменные:
из первого уравнения: ,
из второго уравнения: ,
из третьего уравнения:
Тогда
Из того, что все не
отрицательны, получаем, что переменная t должна
удовлетворять одновременно следующим четырем неравенствам:
Тем самым, мы получили условие .
Не трудно заметить, что при
t = 16.
Ответ:
| В | Наличие | ||||
| 1 | 2 | 3 | |||
| А | 1 | 8 | 5 | 6 | 120 |
| 2 | 4 | 9 | 7 | 180 | |
| Запрос | 70 | 140 | 90 | 300 | |
Пример 2. Компания имеет два товарных склада и трех оптовых
покупателей. Известно, что общий объем запасов на складах составляет 300 тыс.
единиц продукции и совпадает с общим объемом заказов покупателей.
Обозначим через количество товара,
поставляемого со склада покупателю
.
Тогда соответствующая транспортная задача может быть
сформулирована следующим образом.
Минимизировать общую стоимость перевозок:
при условии, что
Получаем задачу линейного программирования, в которой
основные ограничения вследствие того, что транспортная задача сбалансирована,
является равенствами.
Положим и
выразим через u и
v остальные переменные. Имеем
Учитывая, что все перевозки должны получить неотрицательные значения, мы
приходим к задаче
которую можно решить графическим методом.
Выписанные неравенства определяют на плоскости (u,
v) пятиугольник с вершинами (30, 0), (70, 0), (70, 50), (0,
120), (0, 30).
Ответ:
В начало
Источник
