Построить математическую модель следующей задачи о диете
2.1. Задача о диете
Исторические задача о диете является одной из первых задач линейного
программирования.
Постановка задачи – первый и наиболее важный этап построения модели,
способный обеспечить правильное решение проблемы.
Даме необходимо похудеть, за помощью обратилась к подруге.
Построение модели – рассмотрение этого этапа и является главной целью.
Подруга посоветовала перейти на рациональное питание, состоящее из двух
продуктов P и Q.
Суточное питание этими продуктами должно давать не более 14 единиц жира
(чтобы похудеть), но не менее 300 калорий. На упаковке продукта Р
написано, что в одном килограмме этого продукта содержится 15 единиц жира и 150
калорий, а на упаковке с продуктом Q – 4
единицы жира и 200 калорий соответственно. При этом цена 1 килограмма продукта
Р равна 15 руб., а 1 кг продукта Q – 25
руб.
Так как дама была стеснена в средствах, но ее интересовал вопрос: в какой
пропорции нужно брать эти продукты для того, чтобы выдержать условия диеты и
истратить как можно меньше денег?
Перейдем к формализации данной ситуации на языке математических символов.
Обозначим через х количество продукта Р и
через у количество продукта Q, требуемые
для выполнения условий диеты.
Количество единиц жира, содержащегося в х кг продукта
Р и в у кг продукта Q, равно
15х + 4 и по условию диеты не должно превосходить 14:
В свою очередь, количество калорий, содержащихся в х
кг продукта Р и в у кг продукта Q,
равно 150х + 200у и по условию диеты должно быть не меньше 300:
Теперь о стоимости z продуктов.
Она равна
и в соответствии с высказанными пожеланиями должна быть минимальной.
Последнее записывается так:
Тем самым мы получили систему формул:
которую решим графическим способом.
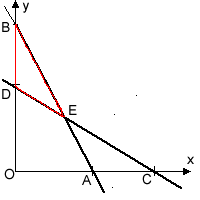
Нас интересует только та ее часть, которая лежит над треугольником
BDE. Вычисляя значения z
во всех трех вершинах этого треугольника
и сравнивая полученные результаты, замечаем, что наименьшее значение (35)
достигается в вершине Е. Таким образом,
и искомая пропорция – 2 : 3.
2.2. Задача о выпуске продукции
Фирма выпускает два вида древесно-стружечных плит – обычные и
улучшенные. При этом производится две основные операции – прессование и отделка.
Требуется указать, какое количество плит каждого типа можно изготовить в течение
месяца так, чтобы обеспечить максимальную прибыль при следующих ограничениях на
ресурсы (материал, время, затраты):
Затраты | Партия из 100 плит | Имеющиеся ресурсы на месяц | |
обычных | улучшенных | ||
| Материал (фунты) Время на прессование (часы) Время на отделку (часы) Средства (деньги) | 20 | 40 | 4000 |
| Прибыль | 80 | 100 | max |
Перейдем к построению математической модели
поставленной задачи. Введем следующие обозначения. Пусть
х – количество партий в 100 плит обычного
вида, изготавливаемых в течение месяца;
у – количество партий в 100 плит
улучшенного качества, изготавливаемых в течение месяца.
Тогда ожидаемую прибыль можно записать так:
Требуется найти такие значения х и у,
подчиненные условиям
для которых
Для того, чтобы найти в первой четверти плоскости хОу
множество точек, координаты (х, у) которых удовлетворяют указанным выше
неравенствам, необходимо сначала построить прямые (по точкам их пересечения с
координатными осями)
а затем, используя точку начала отсчета О(0, 0),
определить соответствующие полуплоскости. Пересечением полученных полуплоскостей
будет четырехугольник ОВМЕ.
Наша целевая функция достигает наибольшего значения в одной
из вершин четырехугольника.
Нам необходимо найти координаты точки М – точки
пересечения прямых EF и АВ, для этого надо
решить систему уравнений
Вычислить значения z в точках
В(0, 100), Е(150, 0), М(100, 50):
Из полученных значений выберем наибольшее и получим ответ:
2.3. Общая задача линейного программирования
В общем случае и число неизвестных , и число ограничений
могут достигать десятков, сотен, тысяч и т.д. Однако набор соответствующих
условий ничем (кроме количества) от рассмотренных выше примеров не отличается.
Это нетрудно заметить уже по общей постановке задачи линейного программирования.
Стандартная математическая формулировка общей задачи
линейного программирования выглядит так: требуется найти экстремальное значение
показателя эффективности (целевой функции)
(линейной функции элементов решения
) при линейных ограничительных
условиях, накладываемых на элементы решения:
где – заданные числа.
Что касается существующих методов решения этой задачи с
числом переменных, больших двух, то в их основе лежат те же идеи, на которые мы
опирались при разработке графического подхода. Конечно, в случае сильного
увеличения числа переменных и ограничений техника получения решения заметно
усложняется, но она опирается на совершенно стандартные, хорошо разработанные
алгоритмы (возникающие трудности связаны лишь с ростом объема необходимых
вычислений).
Общую постановку задачи линейного программирования можно
записать в более компактной форме, если воспользоваться следующим правилом.
Правило сокращенного суммирования. Для обозначения
суммы чисел :
принята такая запись:
где ∑ – знак суммирования, а
k – индекс суммирования.
Это обозначение очень удобно:
А вот как выглядит запись общей задачи линейного
программирования:
2.4. Транспортная задача
Важный тип задач линейного программирования представляет
задача о перевозках. Называется она так потому, что цель этой задачи
заключается в минимизации полной стоимости перевозок известного количества
товаров со складов к потребителю.
Сбалансированная задача – задача о перевозках, в
которой общий объем товаров, готовых к отправлению, в точности равен объему
товаров, который готовы принять в пунктах назначения.
Пример 1. Рассмотрим транспортную задачу, заданную таблицей
| В | Наличие | |||
| 1 | 2 | |||
| А | 1 2 | 1 2 | 2 1 | 20 10 |
| Запрос | 16 | 14 | 30 | |
Решение. Пусть – искомое число единиц
товара, пересылаемого из пункта в пункт
. Тогда данные таблицы можно
представить в следующем виде:
при условии, что
Положим и выразим через
t остальные переменные:
из первого уравнения: ,
из второго уравнения: ,
из третьего уравнения:
Тогда
Из того, что все не
отрицательны, получаем, что переменная t должна
удовлетворять одновременно следующим четырем неравенствам:
Тем самым, мы получили условие .
Не трудно заметить, что при
t = 16.
Ответ:
| В | Наличие | ||||
| 1 | 2 | 3 | |||
| А | 1 | 8 | 5 | 6 | 120 |
| 2 | 4 | 9 | 7 | 180 | |
| Запрос | 70 | 140 | 90 | 300 | |
Пример 2. Компания имеет два товарных склада и трех оптовых
покупателей. Известно, что общий объем запасов на складах составляет 300 тыс.
единиц продукции и совпадает с общим объемом заказов покупателей.
Обозначим через количество товара,
поставляемого со склада покупателю
.
Тогда соответствующая транспортная задача может быть
сформулирована следующим образом.
Минимизировать общую стоимость перевозок:
при условии, что
Получаем задачу линейного программирования, в которой
основные ограничения вследствие того, что транспортная задача сбалансирована,
является равенствами.
Положим и
выразим через u и
v остальные переменные. Имеем
Учитывая, что все перевозки должны получить неотрицательные значения, мы
приходим к задаче
которую можно решить графическим методом.
Выписанные неравенства определяют на плоскости (u,
v) пятиугольник с вершинами (30, 0), (70, 0), (70, 50), (0,
120), (0, 30).
Ответ:
В начало
Источник
ÐÑедположим Ð´Ð»Ñ Ð¾Ð¿ÑеделенноÑÑи, ÑÑо Ð½ÐµÐ¾Ð±Ñ Ð¾Ð´Ð¸Ð¼Ð¾ ÑоÑÑавиÑÑ ÑамÑй деÑевÑй ÑаÑион пиÑÐ°Ð½Ð¸Ñ ÑÑплÑÑ, ÑодеÑжаÑий Ð½ÐµÐ¾Ð±Ñ Ð¾Ð´Ð¸Ð¼Ð¾Ðµ колиÑеÑÑво опÑеделеннÑÑ Ð¿Ð¸ÑаÑелÑнÑÑ Ð²ÐµÑеÑÑв (Ð´Ð»Ñ Ð¿ÑоÑÑоÑÑ, Ñиамина Т и ниаÑина Ð).
ТаблиÑа 8.1
ÐÑÑ Ð¾Ð´Ð½Ñе даннÑе в задаÑе об опÑимизаÑии ÑмеÑи
СодеÑжание в 1 ÑнÑии Ð | СодеÑжание в 1 ÑнÑии С | ÐоÑÑебноÑÑÑ | |
ÐеÑеÑÑво Т | 0,10 мг | 0,25 мг | 1,00 мг |
ÐеÑеÑÑво Ð | 1,00 мг | 0,25 мг | 5,00 мг |
ÐалоÑии | 110,00 | 120,00 | 400,00 |
СÑоимоÑÑÑ 1 ÑнÑии, в ÑенÑÐ°Ñ | 3,8 | 4,2 |
ÐиÑÐµÐ²Ð°Ñ ÑенноÑÑÑ ÑаÑиона (в калоÑиÑÑ ) должна бÑÑÑ Ð½Ðµ менее заданной. ÐÑÑÑÑ Ð´Ð»Ñ Ð¿ÑоÑÑоÑÑ ÑмеÑÑ Ð´Ð»Ñ ÑÑплÑÑ Ð¸Ð·Ð³Ð¾ÑавливаеÑÑÑ Ð¸Ð· двÑÑ Ð¿ÑодÑкÑов – Ри С. ÐзвеÑÑно ÑодеÑжание Ñиамина и ниаÑина в ÑÑÐ¸Ñ Ð¿ÑодÑкÑÐ°Ñ , а Ñакже пиÑаÑелÑÐ½Ð°Ñ ÑенноÑÑÑ Ð Ð¸ С (в калоÑиÑÑ ). СколÑко Ри С надо взÑÑÑ Ð´Ð»Ñ Ð¾Ð´Ð½Ð¾Ð¹ поÑÑии кÑÑиного коÑма, ÑÑÐ¾Ð±Ñ ÑÑплÑÑа полÑÑили Ð½ÐµÐ¾Ð±Ñ Ð¾Ð´Ð¸Ð¼ÑÑ Ð¸Ð¼ Ð´Ð¾Ð·Ñ Ð²ÐµÑеÑÑв Ри Т и калоÑий (или болÑÑе), а ÑÑоимоÑÑÑ Ð¿Ð¾ÑÑии бÑла минималÑна? ÐÑÑ Ð¾Ð´Ð½Ñе даннÑе Ð´Ð»Ñ ÑаÑÑеÑов пÑÐ¸Ð²ÐµÐ´ÐµÐ½Ñ Ð² Табл. 8.1.
ÐадаÑа линейного пÑогÑаммиÑÐ¾Ð²Ð°Ð½Ð¸Ñ Ð¸Ð¼ÐµÐµÑ Ð²Ð¸Ð´:
3,8K+4,2Cð min
0,10K+0,25C≥1,00
1,00K+0,25C≥5,00
110K+120C≥400,00
K≥0
C≥0
Ðе гÑаÑиÑеÑкое ÑеÑение пÑедÑÑавлено на РиÑ. 8.1
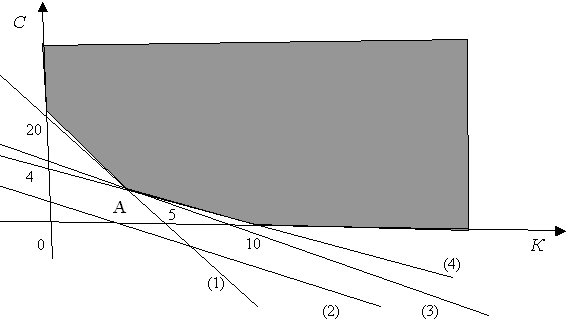
РиÑ. 8.41. ÐÑаÑиÑеÑкое ÑеÑение задаÑи об опÑимизаÑии ÑмеÑи
Ðа ÑиÑ. 8.4 Ñади облегÑÐµÐ½Ð¸Ñ Ð²Ð¾ÑпÑиÑÑÐ¸Ñ ÑеÑÑÑе пÑÑмÑе обознаÑÐµÐ½Ñ Ð½Ð¾Ð¼ÐµÑами (1) – (4). ÐÑÑÐ¼Ð°Ñ (1) опиÑÑваеÑÑÑ ÑÑавнением 1,00K+0,25C=5,00 (огÑаниÑение по веÑеÑÑÐ²Ñ Ð). Ðна пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ, как и показано на ÑиÑÑнке, ÑеÑез ÑоÑки (5, 0) на оÑи абÑÑиÑÑ Ð¸ (0, 20) на оÑи оÑдинаÑ. ÐбÑаÑиÑе внимание, ÑÑо допÑÑÑимÑе знаÑÐµÐ½Ð¸Ñ Ð¿Ð°ÑамеÑÑов (Ð, С) Ð»ÐµÐ¶Ð°Ñ Ð²ÑÑе пÑÑмой (1) или на ней, в оÑлиÑие Ð¾Ñ Ñанее ÑаÑÑмоÑÑеннÑÑ ÑлÑÑаев в пÑедÑдÑÑей пÑоизводÑÑвенной задаÑе линейного пÑогÑаммиÑованиÑ.
ÐÑÑÐ¼Ð°Ñ (2) – ÑÑо пÑÑÐ¼Ð°Ñ 110K+120C=400,00 (огÑаниÑение по калоÑиÑм). ÐбÑаÑим внимание, ÑÑо в облаÑÑи неоÑÑиÑаÑелÑнÑÑ Ð¡ она ÑаÑположена вÑÑÐ´Ñ Ð½Ð¸Ð¶Ðµ пÑÑмой (1). ÐейÑÑвиÑелÑно, ÑÑо веÑно пÑи K=0, пÑÑÐ¼Ð°Ñ (1) пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ ÑеÑез ÑоÑÐºÑ (0, 20), а пÑÑÐ¼Ð°Ñ (2) – ÑеÑез ÑаÑположеннÑÑ Ð½Ð¸Ð¶Ðµ ÑоÑÐºÑ (0, 400/120). ТоÑка пеÑеÑеÑÐµÐ½Ð¸Ñ Ð´Ð²ÑÑ Ð¿ÑÑмÑÑ Ð½Ð°Ñ Ð¾Ð´Ð¸ÑÑÑ Ð¿Ñи ÑеÑении ÑиÑÑÐµÐ¼Ñ ÑÑавнений
1,00K+0,25C=5,00
110K+120C=400,00
Ðз пеÑвого ÑÑÐ°Ð²Ð½ÐµÐ½Ð¸Ñ K=5-0,25C. ÐодÑÑавим во вÑоÑое:
110(5-0,25C)+120C=400, оÑкÑда 550-27,5C+120C=400. СледоваÑелÑно, 150=-92,5C , Ñ. е. ÑеÑение доÑÑигаеÑÑÑ Ð¿Ñи оÑÑиÑаÑелÑном С. ÐÑо и ознаÑаеÑ, ÑÑо пÑи вÑеÑ
положиÑелÑнÑÑ
С пÑÑÐ¼Ð°Ñ (2) Ð»ÐµÐ¶Ð¸Ñ Ð½Ð¸Ð¶Ðµ пÑÑмой (1). ÐнаÑиÑ, еÑли вÑполнено огÑаниÑение по Ð, Ñо обÑзаÑелÑно вÑполнено и огÑаниÑение по калоÑиÑм. ÐÑ ÑÑолкнÑлиÑÑ Ñ Ð½Ð¾Ð²Ñм Ñвлением – некоÑоÑÑе огÑаниÑÐµÐ½Ð¸Ñ Ñ Ð¼Ð°ÑемаÑиÑеÑкой ÑоÑки зÑÐµÐ½Ð¸Ñ Ð¼Ð¾Ð³ÑÑ Ð¾ÐºÐ°Ð·Ð°ÑÑÑÑ Ð»Ð¸Ñними. С ÑкономиÑеÑкой ÑоÑки зÑÐµÐ½Ð¸Ñ Ð¾Ð½Ð¸ необÑ
одимÑ, оÑÑажаÑÑ ÑÑÑеÑÑвеннÑе ÑеÑÑÑ Ð¿Ð¾ÑÑановки задаÑи, но в данном ÑлÑÑае внÑÑÑеннÑÑ ÑÑÑÑкÑÑÑа задаÑи оказалаÑÑ Ñакова, ÑÑо огÑаниÑение по калоÑиÑм не ÑÑаÑÑвÑÐµÑ Ð² ÑоÑмиÑовании допÑÑÑимой облаÑÑи паÑамеÑÑов и наÑ
ождении ÑеÑениÑ.
ÐÑÑÐ¼Ð°Ñ (4) – ÑÑо пÑÑÐ¼Ð°Ñ 0,1K+0,25C=1 (огÑаниÑение по веÑеÑÑÐ²Ñ Ð¢). Ðна пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ, как и показано на ÑиÑÑнке, ÑеÑез ÑоÑки (10, 0) на оÑи абÑÑиÑÑ Ð¸ (0, 4) на оÑи оÑдинаÑ. ÐбÑаÑиÑе внимание, ÑÑо допÑÑÑимÑе знаÑÐµÐ½Ð¸Ñ Ð¿Ð°ÑамеÑÑов (Ð, С) Ð»ÐµÐ¶Ð°Ñ Ð²ÑÑе пÑÑмой (4) или на ней, как и Ð´Ð»Ñ Ð¿ÑÑмой (1).
СледоваÑелÑно, облаÑÑÑ Ð´Ð¾Ð¿ÑÑÑимÑÑ Ð·Ð½Ð°Ñений паÑамеÑÑов (Ð, С) ÑвлÑеÑÑÑ Ð½ÐµÐ¾Ð³ÑаниÑенной ÑвеÑÑ Ñ. Ðз вÑей плоÑкоÑÑи она вÑделÑеÑÑÑ Ð¾ÑÑми кооÑÐ´Ð¸Ð½Ð°Ñ (Ð»ÐµÐ¶Ð¸Ñ Ð² пеÑвом квадÑанÑе) и пÑÑмÑми (1) и (4) (Ð»ÐµÐ¶Ð¸Ñ Ð²ÑÑе ÑÑÐ¸Ñ Ð¿ÑÑмÑÑ , а Ñакже вклÑÑÐ°ÐµÑ Ð³ÑаниÑнÑе оÑÑезки). ÐблаÑÑÑ Ð´Ð¾Ð¿ÑÑÑимÑÑ Ð·Ð½Ð°Ñений паÑамеÑÑов, Ñ. е. ÑоÑек (Ð, С), можно назваÑÑ “неогÑаниÑеннÑм многоÑголÑником”. ÐинимÑм Ñелевой ÑÑнкÑии 3.8K+4,2C Ð¼Ð¾Ð¶ÐµÑ Ð´Ð¾ÑÑигаÑÑÑÑ ÑолÑко в веÑÑÐ¸Ð½Ð°Ñ ÑÑого “многоÑголÑника”. ÐеÑÑин вÑего ÑÑи. ÐÑо пеÑеÑеÑÐµÐ½Ð¸Ñ Ñ Ð¾ÑÑми абÑÑиÑÑ (10, 0) и оÑÐ´Ð¸Ð½Ð°Ñ (0, 20) пÑÑмÑÑ (1) и (4) (в каждом ÑлÑÑае из двÑÑ Ð¿ÐµÑеÑеÑений беÑеÑÑÑ Ñо, коÑоÑое ÑдовлеÑвоÑÑÐµÑ Ð¾Ð±Ð¾Ð¸Ð¼ огÑаниÑениÑм). ТÑеÑÑÑ Ð²ÐµÑÑина – ÑÑо ÑоÑка РпеÑеÑеÑÐµÐ½Ð¸Ñ Ð¿ÑÑмÑÑ (1) и (4), кооÑдинаÑÑ ÐºÐ¾ÑоÑой Ð½Ð°Ñ Ð¾Ð´ÑÑÑÑ Ð¿Ñи ÑеÑении ÑиÑÑÐµÐ¼Ñ ÑÑавнений
0,10K+0,25C=1,00
1,00K+0,25C=5,00
Ðз вÑоÑого ÑÑÐ°Ð²Ð½ÐµÐ½Ð¸Ñ K=5-0,25C, из пеÑвого
0,1(5-0,25C)+0,25C=5,00=0,25C=0,5+0,225C=1, оÑкÑда C=0,5/0,225=20/9 и K=5-5/9=40/9. ÐÑак, A=(20/9,40/9).
ÐÑÑÐ¼Ð°Ñ (3) на РиÑ. 8.5 – ÑÑо пÑÑмаÑ, ÑооÑвеÑÑÑвÑÑÑÐ°Ñ Ñелевой ÑÑнкÑии 3,8K+4,2C. Ðна пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ Ð¼ÐµÐ¶Ð´Ñ Ð¿ÑÑмÑми (1) и (4), задаÑÑими огÑаниÑениÑ, и минимÑм доÑÑигаеÑÑÑ Ð² ÑоÑке Ð, ÑеÑез коÑоÑÑÑ Ð¸ пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ Ð¿ÑÑÐ¼Ð°Ñ (3). СледоваÑелÑно, минимÑм Ñавен 3,8X40/9+4,2X20/9=236/9. ÐадаÑа об опÑимизаÑии ÑмеÑи полноÑÑÑÑ ÑеÑена.
ÐвойÑÑÐ²ÐµÐ½Ð½Ð°Ñ Ð·Ð°Ð´Ð°Ñа, поÑÑÑÐ¾ÐµÐ½Ð½Ð°Ñ Ð¿Ð¾ Ñанее опиÑаннÑм пÑавилам, Ð¸Ð¼ÐµÐµÑ Ð¿ÑиведеннÑй ниже вид (Ð¼Ñ Ð¿Ð¾Ð²ÑоÑÑем здеÑÑ Ð¸ иÑÑ Ð¾Ð´Ð½ÑÑ Ð·Ð°Ð´Ð°ÑÑ Ð¾Ð± опÑимизаÑии ÑмеÑи, ÑÑÐ¾Ð±Ñ Ð½Ð°Ð³Ð»Ñдно пÑодемонÑÑÑиÑоваÑÑ ÑÐµÑ Ð½Ð¾Ð»Ð¾Ð³Ð¸Ñ Ð¿Ð¾ÑÑÑÐ¾ÐµÐ½Ð¸Ñ Ð´Ð²Ð¾Ð¹ÑÑвенной задаÑи):
3,8K+4,2Cð min W1+5W2+400W3ð max
0,10K+0,25C ≥1,00 0,1W1+1,10W2+110W3≤3,8
1,00K+0,25C ≥5,00 0,25W1+0,25W2+120W3≤4,2
110K+120C ≥400,00 W1≥0
K ≥0 W2≥0
C ≥0 W3≥0
ÐинималÑное знаÑение в пÑÑмой задаÑе, как и должно бÑÑÑ, Ñавно макÑималÑÐ½Ð¾Ð¼Ñ Ð·Ð½Ð°ÑÐµÐ½Ð¸Ñ Ð² двойÑÑвенной задаÑе, Ñ. е. оба ÑиÑла ÑÐ°Ð²Ð½Ñ 236/9. ÐнÑеÑпÑеÑаÑÐ¸Ñ Ð´Ð²Ð¾Ð¹ÑÑвеннÑÑ Ð¿ÐµÑеменнÑÑ : W1 – “ÑÑоимоÑÑÑ” единиÑÑ Ð²ÐµÑеÑÑва Т, а W2 – “ÑÑоимоÑÑÑ” единиÑÑ Ð²ÐµÑеÑÑва Ð, измеÑеннÑе “по Ð¸Ñ Ð²ÐºÐ»Ð°Ð´Ñ” в ÑелевÑÑ ÑÑнкÑиÑ. ÐÑи ÑÑом W3=0, поÑколÑÐºÑ Ð¾Ð³ÑаниÑение на ÑиÑло калоÑий никак не ÑÑаÑÑвÑÐµÑ Ð² ÑоÑмиÑовании опÑималÑного ÑеÑениÑ. ÐÑак, W1,W2,W3 – ÑÑо Ñ. н. обÑекÑивно обÑÑловленнÑе оÑенки (по Ð. Ð. ÐанÑоÑовиÑÑ) ÑеÑÑÑÑов (веÑеÑÑв Т и Ð, калоÑий).
Источник
Дама просто приятная решила похудеть и, как это нередко случается, обратилась за советом к подруге. Подруга – дама приятная во всех отношениях, посоветовала ей перейти на рациональное питание, состоящее из двух новомодных продуктов Р и Q.
Дневное питание этими новинками должно давать не более 14 единиц жира (чтобы похудеть), но и не менее 300 калорий (чтобы не сойти с дистанции раньше). На банке с продуктом Р написано, что в одном килограмме этого продукта содержится 15 единиц жира и 150 калорий, а на банке с продуктом Q – 4 единицы жира и 200 калорий соответственно. При этом цена 1 кг продукта Р равна 15 у.е., а 1 кг продукта Q – 25 у.е.
Так как дама просто приятная в это время была несколько стеснена в средствах, то ее интересовал ответ на следующий вопрос: в какой пропорции нужно брать эти удивительные продукты Р и Q для того, чтобы выдержать условия диеты и истратить как можно меньше денег?
1. Построение модели. Обозначим через х количество продукта Р, а через у количество продукта Q, требуемые для выполнения условий диеты.
Количество единиц жира, содержащегося в х кг продукта Р и в у кг продукта Q, равно 15х + 4у и по условию диеты не должно превосходить 14. Поэтому .
В свою очередь, количество калорий, содержащихся в х кг продукта Р и в у кг продукта Q, равно 150х + 200у и должно быть не меньше 300. Значит, .
Теперь о стоимости продуктов. Она равна z(х; у) = 15x + 25y и в соответствии с высказанными пожеланиями должна быть минимальной. Последнее записывается так: z(х; у) = 15x + 25y → min.
Итак, мы получили систему неравенств
которая является математической моделью задачи.
Полученная система неравенств называется системой ограничений задачи, а функция z(х; у) называется целевой функцией задачи.
2. Решение математической задачи, к которой приводит модель. Для решения применим координатно-графический метод.
Решением системы ограничений является многоугольник, полученный путем пересечения областей решений всех неравенств системы. Решением линейного неравенства является одна из полуплоскостей, на которые прямая, соответствующая данному неравенству, делит координатную плоскость. Для определения искомой полуплоскости берется точка, не лежащая на прямой, ее координаты подставляются в неравенство. Если в результате получается верное числовое неравенство, то решением является полуплоскость, содержащая выбранную точку. В противном случае, решением является другая полуплоскость.
Введем на плоскости прямоугольную систему координат хОу и построим многоугольник решений системы ограничений нашей задачи.
Из условий х ≥ 0 и у ≥ 0 вытекает, что все точки, которые удовлетворяют системе ограничений, лежат в первой координатной четверти.
Теперь решим неравенство . Ему соответствует прямая, заданная уравнением , которая проходит через точки и . Для проверки возьмем точку О(0; 0): 15 · 0 + 4 · 0 = 0 ≤ 14. Так как 0 ≤ 14 – верное неравенство, то решением неравенства является полуплоскость, содержащая точку О.
Обращаясь подобным же образом с неравенством , находим точки пересечения прямой с осями координат – точки С(2; 0) и D(0; 1,5). Для проверки также возьмем точку О(0; 0): 150 · 0 + 200 · 0 = 0 ≥ 300. Так как 0 ≥ 300 – неверное числовое неравенство, то решением неравенства является полуплоскость, не содержащая точку О.
Пересечением всех полуплоскостей является треугольник BDK. Точка К является точкой пересечения прямых АВ и CD и имеет координаты .
Теперь среди всех точек треугольника найдем ту, координаты которой удовлетворяют условию минимальности целевой функции z.
Для этого построим так называемую линию нулевого уровня функции z, которая задается уравнением z(x; y) = 0. Будем двигать эту прямую в направлении вектора , координаты которого являются соответствующие коэффициенты целевой функции, до места первой встречи этой прямой с треугольником BDK. Искомой точкой будет точка К . То есть искомые значения х = , у = 1.
3. Интерпретация полученных следствий из математической модели. Таким образом, чтобы выполнить условия диеты и истратить при этом как можно меньше средств, продукты Р и Q нужно брать в отношении х : у = : 1 = 2 : 3. То есть на 2 части продукта Р брать 3 части продукта Q.
Выводы
Модель – это условный образ объекта, построенный для упрощения его исследования.
Конечно, при попытке упрощенного описания ситуации некоторыми обстоятельствами приходится пренебрегать, считая их несущественными. Однако единого взгляда на то, что именно существенно, а что не очень, по-видимому, нет. Можно, например, не обращать внимания на то, что начался дождик. Но одно дело пробежать под накрапывающим дождем сотню метров, и совсем другое – часовая прогулка под таким дождем без зонта.
Предлагая построенную или выбранную нами модель, мы непременно должны указывать пределы, в которых ею можно пользоваться, и предупреждать о том, что нарушение этих ограничений приводит (и, скорее всего, приведет) к серьезным ошибкам. Коротко говоря, у каждой модели есть свой ресурс.
Покупая блузку или рубашку, мы привыкли к наличию меток, на которых указаны максимально допустимая температура глажения, дозволенные виды стирки и т.п. Это, конечно, ни в коей мере не означает, что нам запрещается, взяв докрасна раскаленный утюг, пройтись им по ткани раз-другой. Такое мы сделать можем. Но вот захотим ли мы носить блузку или рубашку после такого глажения?
Таким образом, построение модели опирается на значительное упрощение изучаемой ситуации и, следовательно, к получаемым на ее основе выводам нужно относиться достаточно осторожно – модель может не все.
Вместе с тем, даже весьма грубая на вид идеализация нередко позволяет глубже вникнуть в суть проблемы. Пробуя как-то влиять на параметры модели (выбирать их, управлять ими), мы получаем возможность подвергнуть исследуемое явление качественному анализу и сделать выводы общего характера.
Контрольные вопросы:
1.Что такое модель, моделирование?
2.Какие два подхода различают в моделировании? В чем их особенность?
3.Перечислите типы моделей. Дайте им краткую характеристику.
4.В чем важность математического моделирования?
5. Перечислите этапы математического моделирования. Охарактеризуйте каждый этап.
6.Как можно классифицировать математические модели?
7.Приведите пример задачи математического моделирования.
8. Почему нужно с осторожностью относиться к выводам, полученным на основе модели?
Источник
