Необходимо составить диету состоящую из двух продуктов

Задача 1. Предположим, что фирма имеет 4 фабрики по производству товаров и 5 центров распределения этих товаров. Фабрики характеризуются производственными мощностями (количество единиц продукции, произведенных за день), а центры – потребностями в этих товарах
 Фабрики и центры распределения товаров расположены в разных городах. Стоимость перевозки единицы продукции между ними (в долларах) известна и приведена на рисунке
Фабрики и центры распределения товаров расположены в разных городах. Стоимость перевозки единицы продукции между ними (в долларах) известна и приведена на рисунке

Задача состоит в планировании объемов перевозок таким образом, чтобы минимизировать суммарные транспортные расходы фирмы.
2. Выполнить в Word:

Выполнить в CorelDraw:

Задача 2. Фабрика имеет в своем распоряжении определенное количество ресурсов: рабочую силу, деньги, сырье, оборудование, производственные площади и т. п. Допустим имеются ресурсы трех видов рабочая сила, сырье и оборудование в количестве соответственно 80 (чел/дней), 480 (кг), 130 (станко/часов). Фабрика может выпускать ковры четырех видов. Информация о количестве единиц каждого ресурса необходимых для производства одного ковра каждого вида и доходах, получаемых предприятием от единицы каждого вида товаров, приведена в таблице на рисунке 60. Требуется найти такой план выпуска продукции, при котором общая стоимость продукции будет максимальная.
Ресурсы | Нормы расхода ресурсов на единицу изделия | Наличие ресурсов | |||
Ковер А | Ковер В | Ковер С | Ковер D | ||
Труд | 7 | 2 | 2 | 6 | 80 |
Сырье | 5 | 8 | 4 | 3 | 480 |
Оборудование | 2 | 4 | 1 | 8 | 130 |
Цена (тыс. руб.) | 3 | 4 | 3 | 1 |
Выполнить в Word:

Выполнить в CorelDraw:

Задача 3. Для изготовления четырех видов продукции (А, Б, В, Г) используются три вида ресурсов (сырье, рабочая сила и оборудование). Запасы ресурсов, нормы их расхода на единицу продукции и получаемая прибыль от единицы продукции указаны в таблице, на основании этих данных определите оптимальный план выпуска продукции из условия максимизации прибыли, сформулируйте экономически, запишите и решите задачу, а также определите изменение сырья на -10, оборудования на +12 (оцените раздельное и суммарное влияние этих изменений).
Ресурсы | Нормы расхода | Запас | |||
А | Б | В | Г | ||
1 | 2 | 3 | 4 | 5 | 6 |
Сырье, кг | 3 | 5 | 2 | 4 | 60 |
Раб. сила, чел | 22 | 14 | 18 | 30 | 400 |
Оборудование, станков чел | 10 | 14 | 8 | 16 | 128 |
Прибыль | 30 | 25 | 56 | 48 |
Выполнить в Word:

Выполнить в CorelDraw:
![]()
Задача 4. На трех участках посевных площадей размером в 300, 500 и 400 га могут быть посажены 4 вида сельскохозяйственных культур, которые необходимо вырастить в количестве, соответственно 600, 1500, 220 и 1100 тонн. Матрица (Cij) характеризует себестоимость 1т при выращивании i-й культуры на j-м участке. Составить оптимальный план посева, если урожайность по различным культурам не зависит от участка посева и составляет 30, 40, 20 и 60 ц/га.
30 15 40
Cij = 40 30 25
25 20 30
20 10 25
Выполнить в Word:

Выполнить в CorelDraw:

Задача 5. На трех участках посевных площадей размером в 50, 250 и 100 га могут быть посажены 4 вида сельскохозяйственных культур, которые необходимо вырастить в количестве, соответственно 6000, 1500, 2200 и 1100 тонн. Матрица (Cij) характеризует себестоимость 1т при выращивании i-й культуры на j-м участке. Составить оптимальный план посева, если урожайность по различным культурам не зависит от участка посева и составляет 40, 50, 20 и 70 ц/га.
30 15 40
Cij = 40 30 25
25 20 30
20 10 25
Выполнить в Word:

Выполнить в CorelDraw:

Задача 6. На трех участках посевных площадей размером в 10, 20 и 60 га могут быть посажены 4 вида сельскохозяйственных культур, которые необходимо вырастить в количестве, соответственно 500, 1500, 220 и 1200 тонн. Матрица (Cij) характеризует себестоимость 1т при выращивании i-й культуры на j-м участке. Составить оптимальный план посева, если урожайность по различным культурам не зависит от участка посева и составляет 30, 50, 20 и 80 ц/га.
30 15 40
Cij = 40 30 25
25 20 30
20 10 25
Выполнить в Word:

Выполнить в CorelDraw:

Задача 7. Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности условий можно приготовить не более 800 штук изделий. Рабочий день длится 8 часов. За день можно произвести не более 400 пирожных, пирожков – 1200 (по отдельности).
Стоимость пирожного втрое выше стоимости пирожка. Требуется составить такой дневной план производства, чтобы обеспечить наибольшую выручку.
Выполнить в Word:

Выполнить в CorelDraw:

Задача 8. Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности условий можно приготовить не более 900 штук изделий. Рабочий день длится 8 часов. За день можно произвести не более 500 пирожных, пирожков – 1500 (по отдельности). Перед кондитерским цехом ставится обязательное условие: число пирожных должны быть не меньше числа пирожков.
Стоимость пирожного вдвое выше стоимости пирожка. Требуется составить такой дневной план производства, чтобы обеспечить наибольшую выручку.
Выполнить в Word:

Выполнить в CorelDraw:

Задача 9. На трех мукомольных предприятиях 1, 2, 3 ежедневно производится 110, 190 и 90 т муки. Эта мука потребляется четырьмя хлебозаводами I, II, III, IV, ежедневные потребности которых равны соответственно 80, 60, 170 и 80 т. Тарифы перевозок 1 т муки с мукомольных предприятий на хлебозаводы задаются матрицей 

Составить такой план доставки муки, при котором общая стоимость перевозок являлась бы минимальной.

Выполнить в CorelDraw:

Задача 10. Директор магазина должен составить штатное расписание, т. е. определить, сколько сотрудников, на каких должностях и с каким окладом он должен принять на работу. Общий месячный фонд зарплаты составляет $ 15000.
Построим модель решения этой задачи.
Поясним, что является исходными данными. Казалось бы, что ничего не дано, кроме общего фонда заработной платы. Однако директору магазина известно больше: он знает, что для нормальной работы магазина нужно:
3 уборщицы; 2-4 грузчика; 2 товароведа; 1 секретарь; 5-10 сервисная служба; 8-10 продавцы-консультанты; 1 бухгалтер; 1 директор;
На некоторых должностях число людей может меняться. Например, зная, что найти работников сервисной службы трудно, руководитель может принять решение сократить их число, чтобы увеличить оклад каждого из них.
Итак, директор принимает для себя следующую модель задачи. За основу берется оклад уборщицы, а все остальные вычисляются через нее: во столько раз или на столько-то больше. Говоря математическим языком, каждый оклад является линейной функцией от оклада уборщицы: А*С+В, где С – оклад уборщицы;
А и В – коэффициенты, которые для каждой должности определяются решением совета трудового коллектива.
Допустим, совет решил, что грузчик должен получать в 1,5 раз больше уборщицы
товаровед – в 3 раза больше уборщицы
сервисная служба – на 30 $ больше, чем товаровед
секретарь – в 2 раза больше уборщицы
бухгалтер – на 40 $ больше грузчика
продавец-консультант – в 4 раза больше уборщицы
директор – на 20 $ больше продавца-консультанта

Выполнить в CorelDraw:

Задача 11. Директор автомобильного салона должен составить штатное расписание, т. е. определить, сколько сотрудников, на каких должностях и с каким окладом он должен принять на работу. Общий месячный фонд зарплаты составляет $ 12000.
Для нормальной работы магазина нужно: 4-5 уборщицы; 1 секретарь; 5-10 сервисная служба; 5-8 продавцы-консультанты;
2-3 работники бухгалтерии; 1-3 маркетинговый отдел; 1 гл. бухгалтер; 1 директор.
На некоторых должностях число людей может меняться. Например, зная, что найти работников сервисной службы трудно, руководитель может принять решение сократить их число, чтобы увеличить оклад каждого из них секретарь должен получать в 1,5 раз больше уборщицы
сервисная служба – в 3 раза больше уборщицы
работники бухгалтерии – на 30 $ больше, чем сервисная служба
продавец-консультант – в 2 раза больше уборщицы
гл. бухгалтер – на 40 $ больше секретаря
отдел маркетинга – в 4 раза больше уборщицы
директор – на 20 $ больше отдела маркетинга

Выполнить в CorelDraw:

Задача 12. Директор платной школы должен составить штатное расписание, т. е. определить, сколько сотрудников, на каких должностях и с каким окладом он должен принять на работу. Общий месячный фонд зарплаты составляет $ 8000.
Для нормальной работы школы нужно: 3 уборщицы; 3 повара; 1 завхоз; 5-8 лаборантов; 20-30 учителей; 1 завуч; 1 зам. директора; 1 директор;
На некоторых должностях число людей может меняться. Например, зная, что найти учителей трудно, руководитель может принять решение сократить число учителей, чтобы увеличить оклад каждой из них.
Допустим, совет решил, что повар должен получать в 1,5 раз больше уборщицы
завхоз – в 3 раза больше уборщицы
учитель – на 30 $ больше, чем завхоз
лаборант – в 2 раза больше уборщицы
зам. директора – на 40 $ больше повара
завуч – в 4 раза больше уборщицы
директор – на 20 $ больше завуча

Выполнить в CorelDraw:

Задача 13. Некий завод производит в смену суммарно не более 300 изделий. Необходимо определить при этом ограничении, а также при условии, что должно производиться не менее 30 шт. любого изделия, количество выпускаемых изделий таким образом, чтобы получить максимальный доход.
Рабочий лист имеет вид:


Выполнить в CorelDraw:

Задача 14. Производственные расчеты
Подготовьте лист для расчетов:

Бюджет по первому проекту ограничен суммой 1200000, при этом производственные и фиксированные расходы остаются неизменными, можно изменять только расходы на маркетинг и рекламу, но расходы на маркетинг должны быть не менее 120000, а расходы на рекламу не могут превышать 70000.
Выполнить в Word:

Выполнить в CorelDraw:

Задача 15. Предприятие выпускает 2 вида продукции. Цена единицы 1 вида продукции – 25 000, 2 вида продукции – 50 000. Для изготовления продукции используются три вида сырья, запасы которого 37, 57,6 и 7 условных единиц. Нормы затрат каждого сырья на единицу продукции представлены в следующей таблице.
Продукция | Запасы сырья | |
1-й вид продукции | 2-й вид продукции | |
1,2 | 1,9 | 37 |
2,3 | 1,8 | 57,6 |
0,1 | 0,7 | 7 |
Требуется определить плановое количество выпускаемой продукции таким образом, чтобы стоимость произведенной продукции была максимальной
Выполнить в Word:

Выполнить в CorelDraw:

Задача 16. Сетевая транспортная задача
На складах имеется груз, количество которого определяется в следующей таблице:
Склады | Склад 1 | Склад 2 | Склад 3 |
Наличие груза на складе | 18 | 75 | 31 |
Этот груз необходимо перевезти в пункты назначения в соответствии с таблицей:
Пункты Назначения | Пункт 1 | Пункт 2 |
Потребность груза | 45 | 79 |
Стоимость перевозок определяется таблицей:
Пункт 1 | Пункт 2 | |
Склад 1 | 17 | 6 |
Склад 2 | 12 | 13 |
Склад 3 | 9 | 8 |
Необходимо составить план перевозок так, чтобы стоимость перевозок была минимальной.
Выполнить в Word:

Выполнить в CorelDraw:

Задача 17. Задача на составление диеты
Необходимо составить диету, состоящую из двух продуктов А и Б. Дневное питание этими продуктами должно давать не более 14 единиц жира, но и не менее 300 калорий. В одном килограмме продукта А содержится 15 единиц жира и 150 калорий, а в одном килограмме продукта Б – 4 единицы жира и 200 калорий. При этом цена одного килограмма продукта А равна 15 у. е., а цена одного килограмма продукта Б – 25 у. е. Какое количество продуктов в день необходимо употреблять для соблюдения диеты, чтобы вложенные средства были минимальны?
Выполнить в Word:


Выполнить в CorelDraw:
Задача 18. Задача на максимизацию прибыли.
На основании информации, приведённой в таблице, составить план производства, максимизирующий объём прибыли.

Выполнить в Word:

Выполнить в CorelDraw:

Задача 19. Задача на оптимальное распределение ресурсов
Фабрика выпускает три вида тканей, причём суточное плановое задание составляет не менее 90 м тканей первого вида, 70м — второго и 60 м -> третьего. Суточные ресурсы следующие: 80 единиц производственного оборудования, 850 единиц сырья и 790 единиц электроэнергии, расход которых на один метр тканей представлен в таблице.

Цена за 1 м ткани вида I равна 80 у. е., II – 70 у. е., III – 60 у. е. Определить, сколько метров ткани каждого вида следует выпустить, чтобы общая стоимость выпускаемой продукции была максимальной.
Выполнить в Word:

Выполнить в CorelDraw:

Задача 20. Фабрика имеет в своем распоряжении определенное количество ресурсов: рабочую силу, деньги, сырье, оборудование, производственные площади и т. п.
Допустим имеются ресурсы трех видов рабочая сила, сырье и оборудование в количестве соответственно 80 (чел/дней), 480 (кг), 130 (станко/часов).
Фабрика может выпускать ковры четырех видов. Информация о количестве единиц каждого ресурса необходимых для производства одного ковра каждого вида и доходах, получаемых предприятием от единицы каждого вида товаров, приведена в таблице.
Требуется найти такой план выпуска продукции, при котором общая стоимость продукции будет максимальная.

Выполнить в Word:


Выполнить в CorelDraw:
Задача 21. Завод выпускает продукцию в четырех цехах: A, B, C, D, расположенных на разных территориях. Свою продукцию завод поставляет в шесть магазинов города. Цех A производит 130 тыс. изделий, цех B -90, цех С – 100 и цех D – соответственно 140 тыс. шт. изделий. Плановая потребность магазинов в продукции завода следующая: магазин 1 – 110 тыс. шт. изделий, магазин 2 – 50 тыс. шт., магазин 3 – 30 тыс. шт., магазин 4 – 80 тыс. шт., магазин 5 – 100 тыс. шт. и магазин 6 – 90 тыс. шт. Стоимость перевозки 1 тыс. шт. изделий из цехов в магазины приведена в таблице.
Цеха завода | Магазины | |||||
1 | 2 | 3 | 4 | 5 | 6 | |
A | 2 | 3 | 6 | 8 | 2 | 10 |
B | 8 | 1 | 2 | 3 | 9 | 5 |
C | 7 | 6 | 4 | 1 | 5 | 9 |
D | 2 | 10 | 8 | 5 | 3 | 4 |
Составьте такой план перевозки изделий, при котором расходы на перевозку изделий были бы наименьшими.
Выполнить в Word:

Выполнить в CorelDraw:

Задача 22. Торговая фирма «Весна и осень» включает четыре предприятия и шесть складов в различных регионах страны. Каждый месяц предприятия фирмы производят 100, 15, 90 и 55 ед. продукции. Вся производимая продукция направляется на склады, вместимость которых следующая: 30, 40, 55, 80, 45, и 10 ед. продукции. Издержки транспортировки продукции от предприятий до складов следующие (ден. ед.)
Предприятия фирмы “Весна и осень” | Склады | |||||
1 | 2 | 3 | 4 | 5 | 6 | |
1 | 1 | 5 | 2 | 2 | 1 | 6 |
2 | 3 | 6 | 2 | 4 | 3 | 3 |
3 | 8 | 10 | 4 | 5 | 6 | 8 |
4 | 7 | 3 | 7 | 9 | 1 | 2 |
Определите план перевозок из условия минимизации ежемесячных расходов на транспортировку.
Выполнить в Word:


Выполнить в CorelDraw:
Задача 23. Имеются четыре овощехранилища, расположенные в разных районах города, в которых сосредоточено 10, 20, 35 и 45 т овощей соответственно. Овощи необходимо перевезти четырем потребителям соответственно в количестве 25, 30, 40 и 15 т. Расстояния от хранилищ до потребителей следующие
Хранилище | Потребители | |||
1 | 2 | 3 | 4 | |
1 | 7 | 3 | 3 | 8 |
2 | 7 | 6 | 2 | 7 |
3 | 4 | 7 | 7 | 3 |
4 | 5 | 2 | 4 | 5 |
Затраты на перевозку 1т овощей на 1 км постоянны и равны 20 руб.
Определите план перевозок продукта от хранилищ до потребителей из условия минимизации транспортных расходов.
Выполнить в Word:


Выполнить в CorelDraw:
Источник
ÐÑедположим Ð´Ð»Ñ Ð¾Ð¿ÑеделенноÑÑи, ÑÑо Ð½ÐµÐ¾Ð±Ñ Ð¾Ð´Ð¸Ð¼Ð¾ ÑоÑÑавиÑÑ ÑамÑй деÑевÑй ÑаÑион пиÑÐ°Ð½Ð¸Ñ ÑÑплÑÑ, ÑодеÑжаÑий Ð½ÐµÐ¾Ð±Ñ Ð¾Ð´Ð¸Ð¼Ð¾Ðµ колиÑеÑÑво опÑеделеннÑÑ Ð¿Ð¸ÑаÑелÑнÑÑ Ð²ÐµÑеÑÑв (Ð´Ð»Ñ Ð¿ÑоÑÑоÑÑ, Ñиамина Т и ниаÑина Ð).
ТаблиÑа 8.1
ÐÑÑ Ð¾Ð´Ð½Ñе даннÑе в задаÑе об опÑимизаÑии ÑмеÑи
СодеÑжание в 1 ÑнÑии Ð | СодеÑжание в 1 ÑнÑии С | ÐоÑÑебноÑÑÑ | |
ÐеÑеÑÑво Т | 0,10 мг | 0,25 мг | 1,00 мг |
ÐеÑеÑÑво Ð | 1,00 мг | 0,25 мг | 5,00 мг |
ÐалоÑии | 110,00 | 120,00 | 400,00 |
СÑоимоÑÑÑ 1 ÑнÑии, в ÑенÑÐ°Ñ | 3,8 | 4,2 |
ÐиÑÐµÐ²Ð°Ñ ÑенноÑÑÑ ÑаÑиона (в калоÑиÑÑ ) должна бÑÑÑ Ð½Ðµ менее заданной. ÐÑÑÑÑ Ð´Ð»Ñ Ð¿ÑоÑÑоÑÑ ÑмеÑÑ Ð´Ð»Ñ ÑÑплÑÑ Ð¸Ð·Ð³Ð¾ÑавливаеÑÑÑ Ð¸Ð· двÑÑ Ð¿ÑодÑкÑов – Ри С. ÐзвеÑÑно ÑодеÑжание Ñиамина и ниаÑина в ÑÑÐ¸Ñ Ð¿ÑодÑкÑÐ°Ñ , а Ñакже пиÑаÑелÑÐ½Ð°Ñ ÑенноÑÑÑ Ð Ð¸ С (в калоÑиÑÑ ). СколÑко Ри С надо взÑÑÑ Ð´Ð»Ñ Ð¾Ð´Ð½Ð¾Ð¹ поÑÑии кÑÑиного коÑма, ÑÑÐ¾Ð±Ñ ÑÑплÑÑа полÑÑили Ð½ÐµÐ¾Ð±Ñ Ð¾Ð´Ð¸Ð¼ÑÑ Ð¸Ð¼ Ð´Ð¾Ð·Ñ Ð²ÐµÑеÑÑв Ри Т и калоÑий (или болÑÑе), а ÑÑоимоÑÑÑ Ð¿Ð¾ÑÑии бÑла минималÑна? ÐÑÑ Ð¾Ð´Ð½Ñе даннÑе Ð´Ð»Ñ ÑаÑÑеÑов пÑÐ¸Ð²ÐµÐ´ÐµÐ½Ñ Ð² Табл. 8.1.
ÐадаÑа линейного пÑогÑаммиÑÐ¾Ð²Ð°Ð½Ð¸Ñ Ð¸Ð¼ÐµÐµÑ Ð²Ð¸Ð´:
3,8K+4,2Cð min
0,10K+0,25C≥1,00
1,00K+0,25C≥5,00
110K+120C≥400,00
K≥0
C≥0
Ðе гÑаÑиÑеÑкое ÑеÑение пÑедÑÑавлено на РиÑ. 8.1
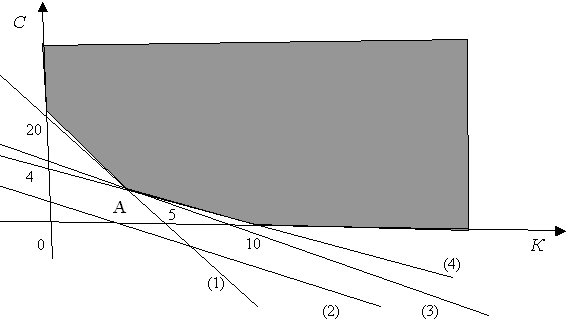
РиÑ. 8.41. ÐÑаÑиÑеÑкое ÑеÑение задаÑи об опÑимизаÑии ÑмеÑи
Ðа ÑиÑ. 8.4 Ñади облегÑÐµÐ½Ð¸Ñ Ð²Ð¾ÑпÑиÑÑÐ¸Ñ ÑеÑÑÑе пÑÑмÑе обознаÑÐµÐ½Ñ Ð½Ð¾Ð¼ÐµÑами (1) – (4). ÐÑÑÐ¼Ð°Ñ (1) опиÑÑваеÑÑÑ ÑÑавнением 1,00K+0,25C=5,00 (огÑаниÑение по веÑеÑÑÐ²Ñ Ð). Ðна пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ, как и показано на ÑиÑÑнке, ÑеÑез ÑоÑки (5, 0) на оÑи абÑÑиÑÑ Ð¸ (0, 20) на оÑи оÑдинаÑ. ÐбÑаÑиÑе внимание, ÑÑо допÑÑÑимÑе знаÑÐµÐ½Ð¸Ñ Ð¿Ð°ÑамеÑÑов (Ð, С) Ð»ÐµÐ¶Ð°Ñ Ð²ÑÑе пÑÑмой (1) или на ней, в оÑлиÑие Ð¾Ñ Ñанее ÑаÑÑмоÑÑеннÑÑ ÑлÑÑаев в пÑедÑдÑÑей пÑоизводÑÑвенной задаÑе линейного пÑогÑаммиÑованиÑ.
ÐÑÑÐ¼Ð°Ñ (2) – ÑÑо пÑÑÐ¼Ð°Ñ 110K+120C=400,00 (огÑаниÑение по калоÑиÑм). ÐбÑаÑим внимание, ÑÑо в облаÑÑи неоÑÑиÑаÑелÑнÑÑ Ð¡ она ÑаÑположена вÑÑÐ´Ñ Ð½Ð¸Ð¶Ðµ пÑÑмой (1). ÐейÑÑвиÑелÑно, ÑÑо веÑно пÑи K=0, пÑÑÐ¼Ð°Ñ (1) пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ ÑеÑез ÑоÑÐºÑ (0, 20), а пÑÑÐ¼Ð°Ñ (2) – ÑеÑез ÑаÑположеннÑÑ Ð½Ð¸Ð¶Ðµ ÑоÑÐºÑ (0, 400/120). ТоÑка пеÑеÑеÑÐµÐ½Ð¸Ñ Ð´Ð²ÑÑ Ð¿ÑÑмÑÑ Ð½Ð°Ñ Ð¾Ð´Ð¸ÑÑÑ Ð¿Ñи ÑеÑении ÑиÑÑÐµÐ¼Ñ ÑÑавнений
1,00K+0,25C=5,00
110K+120C=400,00
Ðз пеÑвого ÑÑÐ°Ð²Ð½ÐµÐ½Ð¸Ñ K=5-0,25C. ÐодÑÑавим во вÑоÑое:
110(5-0,25C)+120C=400, оÑкÑда 550-27,5C+120C=400. СледоваÑелÑно, 150=-92,5C , Ñ. е. ÑеÑение доÑÑигаеÑÑÑ Ð¿Ñи оÑÑиÑаÑелÑном С. ÐÑо и ознаÑаеÑ, ÑÑо пÑи вÑеÑ
положиÑелÑнÑÑ
С пÑÑÐ¼Ð°Ñ (2) Ð»ÐµÐ¶Ð¸Ñ Ð½Ð¸Ð¶Ðµ пÑÑмой (1). ÐнаÑиÑ, еÑли вÑполнено огÑаниÑение по Ð, Ñо обÑзаÑелÑно вÑполнено и огÑаниÑение по калоÑиÑм. ÐÑ ÑÑолкнÑлиÑÑ Ñ Ð½Ð¾Ð²Ñм Ñвлением – некоÑоÑÑе огÑаниÑÐµÐ½Ð¸Ñ Ñ Ð¼Ð°ÑемаÑиÑеÑкой ÑоÑки зÑÐµÐ½Ð¸Ñ Ð¼Ð¾Ð³ÑÑ Ð¾ÐºÐ°Ð·Ð°ÑÑÑÑ Ð»Ð¸Ñними. С ÑкономиÑеÑкой ÑоÑки зÑÐµÐ½Ð¸Ñ Ð¾Ð½Ð¸ необÑ
одимÑ, оÑÑажаÑÑ ÑÑÑеÑÑвеннÑе ÑеÑÑÑ Ð¿Ð¾ÑÑановки задаÑи, но в данном ÑлÑÑае внÑÑÑеннÑÑ ÑÑÑÑкÑÑÑа задаÑи оказалаÑÑ Ñакова, ÑÑо огÑаниÑение по калоÑиÑм не ÑÑаÑÑвÑÐµÑ Ð² ÑоÑмиÑовании допÑÑÑимой облаÑÑи паÑамеÑÑов и наÑ
ождении ÑеÑениÑ.
ÐÑÑÐ¼Ð°Ñ (4) – ÑÑо пÑÑÐ¼Ð°Ñ 0,1K+0,25C=1 (огÑаниÑение по веÑеÑÑÐ²Ñ Ð¢). Ðна пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ, как и показано на ÑиÑÑнке, ÑеÑез ÑоÑки (10, 0) на оÑи абÑÑиÑÑ Ð¸ (0, 4) на оÑи оÑдинаÑ. ÐбÑаÑиÑе внимание, ÑÑо допÑÑÑимÑе знаÑÐµÐ½Ð¸Ñ Ð¿Ð°ÑамеÑÑов (Ð, С) Ð»ÐµÐ¶Ð°Ñ Ð²ÑÑе пÑÑмой (4) или на ней, как и Ð´Ð»Ñ Ð¿ÑÑмой (1).
СледоваÑелÑно, облаÑÑÑ Ð´Ð¾Ð¿ÑÑÑимÑÑ Ð·Ð½Ð°Ñений паÑамеÑÑов (Ð, С) ÑвлÑеÑÑÑ Ð½ÐµÐ¾Ð³ÑаниÑенной ÑвеÑÑ Ñ. Ðз вÑей плоÑкоÑÑи она вÑделÑеÑÑÑ Ð¾ÑÑми кооÑÐ´Ð¸Ð½Ð°Ñ (Ð»ÐµÐ¶Ð¸Ñ Ð² пеÑвом квадÑанÑе) и пÑÑмÑми (1) и (4) (Ð»ÐµÐ¶Ð¸Ñ Ð²ÑÑе ÑÑÐ¸Ñ Ð¿ÑÑмÑÑ , а Ñакже вклÑÑÐ°ÐµÑ Ð³ÑаниÑнÑе оÑÑезки). ÐблаÑÑÑ Ð´Ð¾Ð¿ÑÑÑимÑÑ Ð·Ð½Ð°Ñений паÑамеÑÑов, Ñ. е. ÑоÑек (Ð, С), можно назваÑÑ “неогÑаниÑеннÑм многоÑголÑником”. ÐинимÑм Ñелевой ÑÑнкÑии 3.8K+4,2C Ð¼Ð¾Ð¶ÐµÑ Ð´Ð¾ÑÑигаÑÑÑÑ ÑолÑко в веÑÑÐ¸Ð½Ð°Ñ ÑÑого “многоÑголÑника”. ÐеÑÑин вÑего ÑÑи. ÐÑо пеÑеÑеÑÐµÐ½Ð¸Ñ Ñ Ð¾ÑÑми абÑÑиÑÑ (10, 0) и оÑÐ´Ð¸Ð½Ð°Ñ (0, 20) пÑÑмÑÑ (1) и (4) (в каждом ÑлÑÑае из двÑÑ Ð¿ÐµÑеÑеÑений беÑеÑÑÑ Ñо, коÑоÑое ÑдовлеÑвоÑÑÐµÑ Ð¾Ð±Ð¾Ð¸Ð¼ огÑаниÑениÑм). ТÑеÑÑÑ Ð²ÐµÑÑина – ÑÑо ÑоÑка РпеÑеÑеÑÐµÐ½Ð¸Ñ Ð¿ÑÑмÑÑ (1) и (4), кооÑдинаÑÑ ÐºÐ¾ÑоÑой Ð½Ð°Ñ Ð¾Ð´ÑÑÑÑ Ð¿Ñи ÑеÑении ÑиÑÑÐµÐ¼Ñ ÑÑавнений
0,10K+0,25C=1,00
1,00K+0,25C=5,00
Ðз вÑоÑого ÑÑÐ°Ð²Ð½ÐµÐ½Ð¸Ñ K=5-0,25C, из пеÑвого
0,1(5-0,25C)+0,25C=5,00=0,25C=0,5+0,225C=1, оÑкÑда C=0,5/0,225=20/9 и K=5-5/9=40/9. ÐÑак, A=(20/9,40/9).
ÐÑÑÐ¼Ð°Ñ (3) на РиÑ. 8.5 – ÑÑо пÑÑмаÑ, ÑооÑвеÑÑÑвÑÑÑÐ°Ñ Ñелевой ÑÑнкÑии 3,8K+4,2C. Ðна пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ Ð¼ÐµÐ¶Ð´Ñ Ð¿ÑÑмÑми (1) и (4), задаÑÑими огÑаниÑениÑ, и минимÑм доÑÑигаеÑÑÑ Ð² ÑоÑке Ð, ÑеÑез коÑоÑÑÑ Ð¸ пÑÐ¾Ñ Ð¾Ð´Ð¸Ñ Ð¿ÑÑÐ¼Ð°Ñ (3). СледоваÑелÑно, минимÑм Ñавен 3,8X40/9+4,2X20/9=236/9. ÐадаÑа об опÑимизаÑии ÑмеÑи полноÑÑÑÑ ÑеÑена.
ÐвойÑÑÐ²ÐµÐ½Ð½Ð°Ñ Ð·Ð°Ð´Ð°Ñа, поÑÑÑÐ¾ÐµÐ½Ð½Ð°Ñ Ð¿Ð¾ Ñанее опиÑаннÑм пÑавилам, Ð¸Ð¼ÐµÐµÑ Ð¿ÑиведеннÑй ниже вид (Ð¼Ñ Ð¿Ð¾Ð²ÑоÑÑем здеÑÑ Ð¸ иÑÑ Ð¾Ð´Ð½ÑÑ Ð·Ð°Ð´Ð°ÑÑ Ð¾Ð± опÑимизаÑии ÑмеÑи, ÑÑÐ¾Ð±Ñ Ð½Ð°Ð³Ð»Ñдно пÑодемонÑÑÑиÑоваÑÑ ÑÐµÑ Ð½Ð¾Ð»Ð¾Ð³Ð¸Ñ Ð¿Ð¾ÑÑÑÐ¾ÐµÐ½Ð¸Ñ Ð´Ð²Ð¾Ð¹ÑÑвенной задаÑи):
3,8K+4,2Cð min W1+5W2+400W3ð max
0,10K+0,25C ≥1,00 0,1W1+1,10W2+110W3≤3,8
1,00K+0,25C ≥5,00 0,25W1+0,25W2+120W3≤4,2
110K+120C ≥400,00 W1≥0
K ≥0 W2≥0
C ≥0 W3≥0
ÐинималÑное знаÑение в пÑÑмой задаÑе, как и должно бÑÑÑ, Ñавно макÑималÑÐ½Ð¾Ð¼Ñ Ð·Ð½Ð°ÑÐµÐ½Ð¸Ñ Ð² двойÑÑвенной задаÑе, Ñ. е. оба ÑиÑла ÑÐ°Ð²Ð½Ñ 236/9. ÐнÑеÑпÑеÑаÑÐ¸Ñ Ð´Ð²Ð¾Ð¹ÑÑвеннÑÑ Ð¿ÐµÑеменнÑÑ : W1 – “ÑÑоимоÑÑÑ” единиÑÑ Ð²ÐµÑеÑÑва Т, а W2 – “ÑÑоимоÑÑÑ” единиÑÑ Ð²ÐµÑеÑÑва Ð, измеÑеннÑе “по Ð¸Ñ Ð²ÐºÐ»Ð°Ð´Ñ” в ÑелевÑÑ ÑÑнкÑиÑ. ÐÑи ÑÑом W3=0, поÑколÑÐºÑ Ð¾Ð³ÑаниÑение на ÑиÑло калоÑий никак не ÑÑаÑÑвÑÐµÑ Ð² ÑоÑмиÑовании опÑималÑного ÑеÑениÑ. ÐÑак, W1,W2,W3 – ÑÑо Ñ. н. обÑекÑивно обÑÑловленнÑе оÑенки (по Ð. Ð. ÐанÑоÑовиÑÑ) ÑеÑÑÑÑов (веÑеÑÑв Т и Ð, калоÑий).
Источник
