Фирма занимается составлением диеты содержащей по крайней мере 20 ед белков
Оптимизация в Excel
В старших классах школы при изучении
Excel рассматривается тема
«Оптимизация», для которой можно
использовать первые задачи главы 11
сборника примеров и задач С.М. Лавренова.
Доступное изложение материала в сборнике
и практическая направленность задач
всегда приводит к хорошему усвоению
материала.
Здесь представлено решение трех задач
сборника. Задачи решаются учениками
самостоятельно после объяснения первого
примера главы «Оптимизация» сборника
(Лавренов С.М. «Excel: Сборник
примеров и задач.- М.: Финансы и статистика,
2000.)
Перед объяснением примера нужно
рассказать о том, что в Excel
имеется надстройка «Поиск решения»,
которая позволяет решать задачи отыскания
наибольших и наименьших значений, а
также решать уравнения.
В начале надо убедиться, что Excel
использует надстройку «Поиск решения».
В меню «Сервис» найдем команду «Поиск
решения». Если ее нет, надстройку нужно
установить. Для этого в меню «Сервис»
выбираем команду «Надстройки». В
диалоговом окне находим в списке
надстроек «Поиск решения» и устанавливаем
слева от него флажок. В дальнейшем «Поиск
решения» будет устанавливаться
автоматически, пока мы не снимем флажок
в окне «Надстройки».
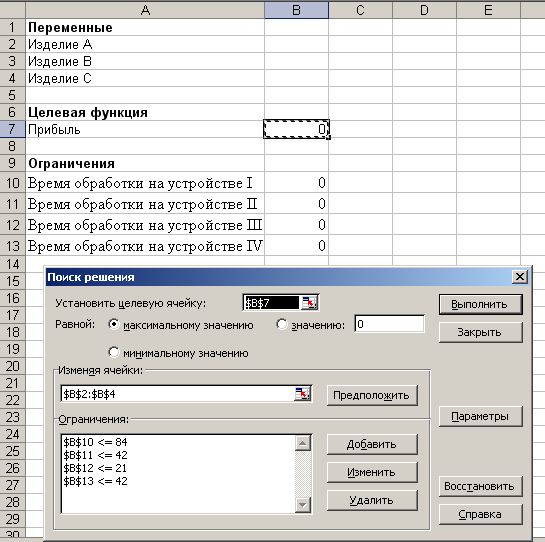
Задача1. Фирма производит три вида
продукции (A, B,
C), для выпуска каждого
требуется определенное время обработки
на всех четырех устройствах I,
II, III, IV
(Рис.1).
Вид продукции | Время | Прибыль, | |||
I | II | III | IV | ||
A | 1 | 3 | 1 | 2 | 3 |
B | 6 | 1 | 3 | 3 | 6 |
C | 3 | 3 | 2 | 4 | 4 |
Рис.1
Пусть время работы на устройствах
соответственно 84, 42, 21 и 42 часа. Определить,
какую продукцию и в каких количествах
стоит производить для максимизации
прибыли. (Рынок сбыта для каждого продукта
неограничен).
Решение. Составим математическую
модель. Обозначим: X –
количество изделий модели А, выпускаемых
в течение недели, Y –
количество изделий модели B,
Z – количество изделий
модели C. Прибыль от этих
изделий равна 3X+6Y+4Z.
Эту прибыль нужно максимизировать.
Функция, для которой ищется экстремум
(максимум или минимум), носит название
целевой функции. Беспредельному
увеличению количества изделий препятствуют
ограничения. В нашем случае ограничено
время обработки на четырех устройствах,
отсюда неравенства:
I устройство – 1X+6Y+3Z
II устройство – 3X+1Y+3Z
III устройство – 1X+3Y+2Z
IV устройство – 2X+3Y+4Z
Кроме того, количество изделий –
неотрицательное число, поэтому X
≥ 0, Y ≥ 0, Z
≥ 0.
Формально наша задача оптимизации
записывается так:
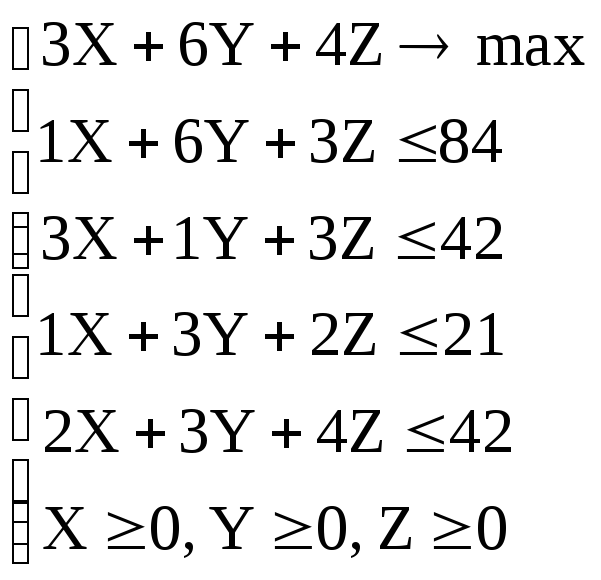
Теперь решим эту задачу в Excel.
Создадим новую рабочую книгу, сохраним
ее под именем Оптимизация.xls.
Введем в ячейки рабочего листа информацию
(рис. 2).
A | B | C | D |
1 | Переменные | ||
2 | Изделие А | X | |
3 | Изделие В | Y | |
4 | Изделие С | Z | |
5 | |||
6 | Целевая функция | ||
7 | Прибыль | =3*X+6*Y+4*Z | |
8 | |||
9 | Ограничения | ||
10 | Время обработки на | =1*X+6*Y+3*Z | <= 84 |
11 | Время обработки на | =3*X+1*Y+3*Z | <=42 |
12 | Время обработки на | =1*X+3*Y+2*Z | <=21 |
13 | Время обработки на | =2*X+3*Y+4*Z | <=42 |
Рис.2
Ячейкам B2, B3
и B4 присвойте имена X,
Y, Z командой
Вставка-Имя-Присвоить. В ячейках С6, С10,
С11, С12 представлены формулы, занесенные
в соответствующие ячейки столбца В.
Выделим ячейку, в которой вычисляется
целевая функция и выполним Поиск решения.
В диалоговом окне в поле ввода «Установить
целевую ячейку:» уже содержится адрес
ячейки с целевой функцией $B$7.
Установим переключатель: «Равным
максимальному значению». Перейдем к
полю ввода «Изменяя ячейки:» и выделим
блок $B$2: $B$4.
Перейдем ко вводу ограничений. Щелкнем
кнопку «Добавить». Появится диалоговое
окно «Добавление ограничения». В поле
ввода «Ссылка на ячейку:» укажем $B$10.
Правее расположен выпадающий список с
условными операторами (раскройте его
и посмотрите). Выберем условие <= . В
поле «Ограничение:» введем число 84. У
нас есть еще три ограничения, поэтому,
не выходя из этого диалогового окна,
щелкаем последовательно кнопку «Добавить»
и вводим соответствующие ограничения
$B$11 <= 42, $B$12<=21,
$B$13<=42. После ввода всех
ограничений нажимаем «ОК». Мы вновь
оказываемся в диалоговом окне «Поиск
решения» (рис. 3):

Рис.3
Щелкнем кнопку «Параметры». Мы оказываемся
в диалоговом окне «Параметры поиска
решения». Чтобы узнать назначение полей
ввода этого окна, щелкнем кнопку
«Справка». Менять в этом окне ничего не
будем, только установим два флажка:
«Линейная модель» (так как наши ограничения
и целевая функция являются линейными
по переменным X и Y)
и «Неотрицательные значения» (для
переменных X и Y).
Мы подготовили задачу оптимизации.
Нажимаем кнопку «Выполнить». Появляется
диалоговое окно «Результаты поиска
решения». В нем мы читаем сообщение
«Решение найдено. Все ограничения и
условия оптимальности выполнены». На
выбор предлагаются варианты: «Сохранить
найденное решение» или «Восстановить
исходные значения». Выбираем первое.
Можно вывести отчеты: по результатам,
по устойчивости, по пределам. Можно
выполнить их все, чтобы иметь представление,
какая информация в них размещена. Отчеты
не комментируются учителем, поскольку
их полное понимание требует существенного
углубления в методы оптимизации.
После нажатия «ОК» вид таблицы меняется:
в ячейках X и Y
появляются оптимальные значения. Ответ:
максимальная прибыль составляет 55, 125.
Задача 2. Фирма производит два продукта
А и В, рынок сбыта которых неограничен.
Каждый продукт должен быть обработан
каждой машиной I, II,
III. Время обработки в часах
для каждого из изделий приведено на
рис.4:
I | II | III | |
A | 0,5 | 0,4 | 0,2 |
B | 0,25 | 0,3 | 0,4 |
Рис. 4
Время работы машин I, II,
III соответственно 40, 36 и
36 часов в неделю. Прибыль от изделий А
и В составляет соответственно 5 и 3
доллара. Фирме надо определить недельные
нормы выпуска изделий А и В, максимизирующие
прибыль.
Окно решения:
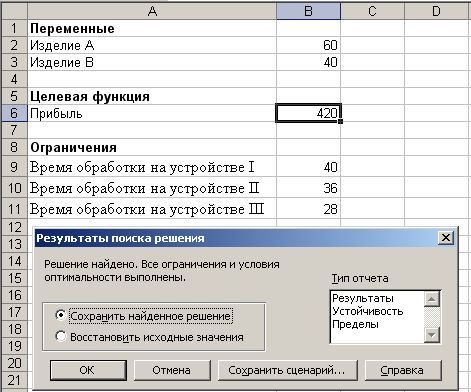
Рис.5
Задача 3. Фирма занимается составлением
диеты, содержащей по крайней мере 20
единиц белков, 30 единиц углеводов, 10
единиц жиров и 40 единиц витаминов. Как
дешевле всего достичь этого при указанных
на рис.4 ценах (в рублях) на 1 кг (или 1 л)
пяти имеющихся продуктов?
Хлеб | Соя | Сушеная рыба | Фрукты | Молоко | |
Белки | 2 | 12 | 10 | 1 | 2 |
Углеводы | 12 | 4 | 3 | ||
Жиры | 1 | 8 | 3 | 4 | |
Витамины | 2 | 2 | 4 | 6 | 2 |
Цена | 12 | 36 | 32 | 18 | 10 |
Рис.6
Решение:
Выполняем ввод данных:
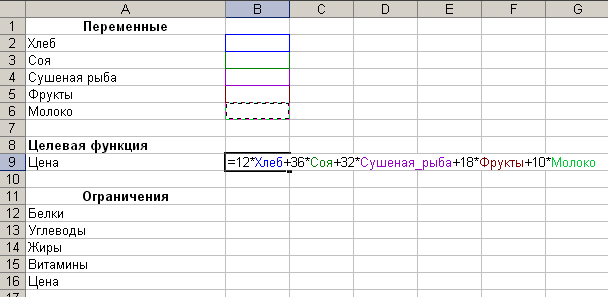
Рис.7
Заполняем поля диалогового окна Поиска
решения:
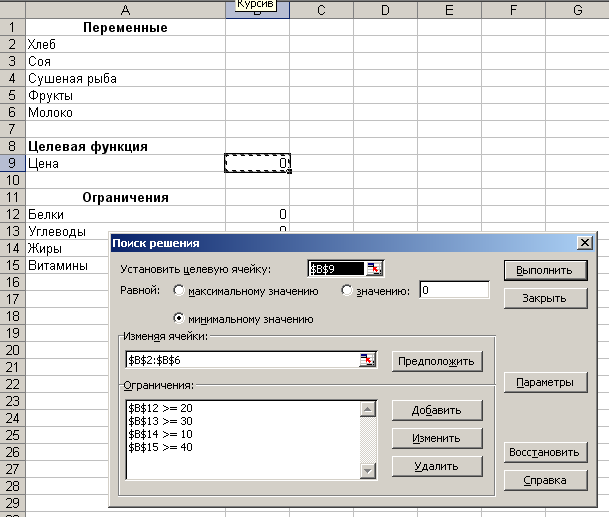
Рис.8
Получаем результат:
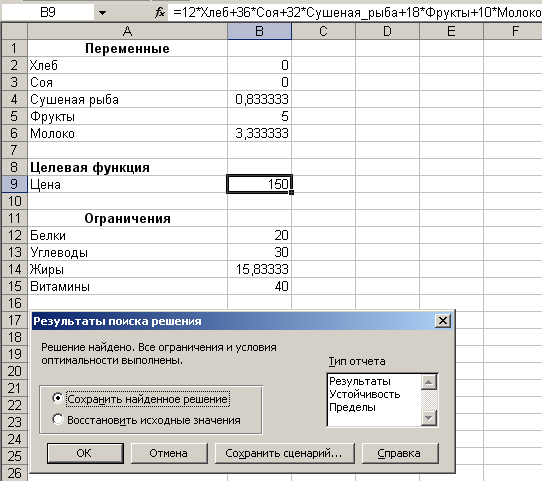
Рис. 9
Источник
Общие сведения
Различные аспекты оптимизации занимают очень важное место в бизнесе и деятельности современных организаций и предприятий. С подобными задачами в своей повседневной работе сталкиваются менеджеры, экономисты, финансисты, фермеры и др. Проблемы оптимизации присутствуют в самых различных процессах производства:
· поставка сырья;
· оптимальный выпуск продукции;
· оптимальное управление запасами;
· оптимальное распределение ресурсов;
· планирования инвестиций;
· оптимальный рацион (смесь, сплав);
· назначение на должность;
· оптимальная замена оборудования и т. д.
Модели всех задач на оптимизацию состоят из следующих элементов:
1. Переменные – неизвестные величины, которые нужно найти при решении задачи.
2. Целевая функция – величина, которая зависит от переменных и является целью, ключевым показателем эффективности или оптимальности модели.
3. Ограничения – условия, которым должны удовлетворять переменные.
Пример
Фирма занимается составлением диеты, которая должна содержать по крайней мере 20 единиц белков, 30 единиц углеводов, 10 единиц жиров и 40 единиц витаминов. Как дешевле всего достичь этого при указанных в таблице ценах (ден. ед.) за 1 кг (или 1 л) пяти имеющихся продуктов?
| Хлеб | Соя | Сушеная рыба | Фрукты | Молоко | |
| Белки | |||||
| Углеводы | |||||
| Жиры | |||||
| Витамины | |||||
| Цена |
Рассмотрим экономико-математическую модель решения данной задачи.
1. Найти количество каждого продукта x, y, z, t, f ,
где
x – количество хлеба,
y – количество сои,
z – количество сушеной рыбы,
t – количество фруктов,
f – количество молока,
2. При котором общая стоимость S=12*x+36*y+32*z+ 18*t+10*f – min
3. При ограничениях:
количество белков = 12*x+12*y+10*z+ 1*t+2*f >=20;
количество углеводов = 12*x+0*y+0*z+ 4*t+3*f >=30;
количество жиров = 1*x+8*y+3*z+ 0*t+4*f >=10;
количество витаминов = 2*x+2*y+4*z+ 6*t+2*f >=40;
и предельных условиях: x, y, z, t, f >=0.
Рассмотрим этапы реализации данной задачи в MS Excel.
В Excel необходимо создать таблицу с формулами, которые связывают план, ограничения и целевую функцию Стоимость (рис. 2.2):
Рис. 2.2. Таблица с исходными данными и формульными зависимостями
В столбец «Вошло» в каждую ячейку вводится формула вычисления количества компонентов, вошедших в диету:
=СУММПРОИЗВ(Норма; План).
В целевую ячейку «Стоимость» вводится формула:
=СУММПРОИЗВ(Цена; План).
Программа Поиск решений запускается командой Сервис – Поиск решения. В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводятся соответствующие данные (рис. 2.3).
Рис. 2.3. Окно Поиск решения
Так как это линейная модель (целевая функция S является линейной), то необходимо установить в окне Параметры поиска решений переключатель в позицию Линейная модель. После нажатия на кнопку Выполнить в появившемся окне Результаты поиска решения укажите Отчет по устойчивости. Результаты поиска решения и полученный отчет представлены на рисунках 2.4 и 2.5.
Рис. 2.5. Отчет по устойчивости
Отчет по устойчивости отражает чувствительность структуры полученного плана до изменений начальных данных и дальнейшие действия менеджера с целью улучшения результатов. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел.
1. Результирующее значение – оптимальный план задачи.
В данной конкретной задаче оптимальный рацион минимальной стоимости 150 д. ед. состоит из 0,83 кг. сушеной рыбы, 5 кг. фруктов и 3,33 л. молока.
2. Нормированная стоимость неизвестных плана указывает, как изменится стоимость рациона при желании добавить в его состав «невыгодный» продукт, например, единица хлеба в рационе увеличит его стоимость на 0,2 д. ед., единица сои – на 4,6 д. ед.
3. Коэффициенты целевой функции.
4, 5. Границы изменений значений коэффициентов целевой функции при условии, что количество оптимальной продукции (план) не изменится. Например, если целевой коэффициент Фруктов (КФ) равен 18 (цена за 1 кг. товара), то изменяя его в рамках 18-0,22<КФ<18+2, 17,78<КФ<20 план не изменится, но значения стоимости может уменьшиться или увеличиться.
6. Количество использованных ресурсов;
7. Теневые цены показывают уровень влияния значения норм (в сравнении с другими ресурсами) на стоимость рациона относительно ее увеличения. В данном примере нормы на состав витаминов более «влиятельные» на стоимость, чем белки (2,5>2,2).
Например, увеличить норму витаминов на 1 единицу (до 41), то стоимость увеличиться на 2,5 д. ед. и будет составлять 152,5 д. ед.
8. Нормы белков, жиров, углеводов и витаминов в дневном рационе. Соответствуют условию задачи.
9, 10. Задают диапазон для 8, в котором действует теневая цена 7 (аналогично 4, 5).
Варианты заданий
1. Фирма производит три вида изделий – А, В и С. Для их выпуска требуется обработка на станках I, II, III, IV. Время обработки каждого изделия на станках приведено в таблице.
| Изделие | Время обработки, ч | Прибыль, $ | |
| I | II | III | IV |
| А | |||
| В | |||
| С |
Составить план выпуска изделий дающий максимальную прибыль, если известно, что фонд рабочего времени станков соответственно равен 84, 42, 21 и 24 часа.
2. Фирме для производства требуется уголь с содержанием фосфора не более 0.03% и с примесью пепла не более 3.25%. Доступны три сорта угля – А, В и С, параметры которых приведены в таблице.
| Сорт угля | Содержание фосфора, % | Содержание пепла, % | Цена, $ |
| А | 0,06 | 2,0 | |
| В | 0,04 | 4,0 | |
| С | 0,02 | 3,0 |
Составить из указанных сортов такую смесь, чтобы она удовлетворяла требованиям производства по содержанию фосфора и пепла и имела минимальную цену.
3. Фирма производит два продукта А и В, рынок сбыта которых неограничен. Каждый продукт должен быть обработан каждой машиной I, II, III. Время обработки в часах для каждого из изделий А и В приведено в таблице.
| I | II | III | |
| А | 0,5 | 0,4 | 0,2 |
| В | 0,25 | 0,3 | 0,4 |
Недельный фонд рабочего времени машин I, II, III равен соответственно 40, 36 и 36 часам. Прибыль от изделий А и В составляет соответственно 5 и 3 доллара. Фирме надо определить недельные нормы выпуска изделий А и В, максимизирующие прибыль.
4. На кондитерскую фабрику г. Ступино перед Новым годом поступили заказы на подарочные наборы конфет из трех магазинов. Возможные варианты наборов, их стоимость и оставшиеся товарные запасы на фабрике представлены в таблице.
Определить оптимальное количество подарочных наборов, которые фабрика может предложить магазинам и обеспечить максимальный доход от продажи.
| Наименование конфет | Вес конфет в наборе, кг | Запасы конфет, кг | ||
| А | В | С | ||
| «Сникерс» | 0,3 | 0,2 | 0,4 | |
| «Марс» | 0,2 | 0,3 | 0,2 | |
| «Баунти» | 0,2 | 0,1 | ОД | |
| Цена, руб. |
5. В контейнер упакованы комплектующие изделия трех типов. Стоимость и вес одного изделия составляют 400 руб.и 12 кг для первого типа, 500 руб.и 16 кг для второго типа, 600 руб.и 15 кг для третьего типа. Общий вес комплектующих равен 326 кг. Определить максимальную и минимальную возможную суммарную стоимость находящихся в контейнере комплектующих изделий.
6. Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель выпускается на отдельной технологической линии. Максимальная производительность линий составляет 60 и 75 радиоприемников в сутки. На приемники первой модели расходуется 10 типовых электронных схем, а на вторую – 8 схем. Суточный запас схем равен 800 единиц. Прибыль от реализации одного радиоприемника первой и второй модели равна соответственно 30 и 20$. Определить оптимальный суточный объем производства радиоприемников первой и второй моделей.
7. Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Суточный фонд машинного времени каждого станка равен 10 часов. Время обработки и прибыль от продажи каждого изделия приведены в таблице.
| Изделие | Время обработки одного изделия, мин | Прибыль, $ |
| Станок 1 | Станок 2 | Станок 3 |
Найти оптимальный объем производства изделий каждого вида.
8. Фирма производит два вида продукции – А и В. Объем сбыта продукции А составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции используется одно и то же сырье, суточный запас которого равен 100 кг. Расход сырья на единицу продукции А составляет 2 кг, а на единицу продукции В – 4 кг. Цены на продукцию А и В равны соответственно 20 и 40$. Составить план распределения сырья для изготовления продукции А и В так, чтобы затраты были минимальные.
9. Кондитерская фабрика в Покрове освоила выпуск новых видов шоколада «Лунная начинка» и «Малиновый дождик», спрос на которые составляет соответственно не более 12 тонн и 7,7 тонны в месяц. По причине занятости трех цехов выпуском традиционных видов шоколада, каждый цех может выделить только ограниченный ресурс времени в месяц. В силу специфики технологического оборудования затраты времени на производство шоколада разные и представлены в таблице.
| Номер цеха | Время на производство шоколада, ч | Время, отведенное цехами под производство, ч/мес | |
| | «Лунная начинка» | «Малиновый дождик» | |
| I | |||
| II | |||
| III | |||
| Оптовая цена, руб./т. |
Определить оптимальный объем выпуска шоколада, обеспечивающий максимальную выручку от продажи.
10. Фирма решила открыть на основе технологии производства чешского стекла, фарфора и хрусталя линию по изготовлению ваз и графинов и их декорирование. Затраты сырья на производство этой продукции представлены в таблице.
| Сырье | Расход сырья на производство, г | Поставки сырья в неделю, кг | |
| ваза | графин | ||
| Кобальт | |||
| Сусальное 24-каратное золото | |||
| Оптовая цена, руб. /шт. |
Определите оптимальный объем выпуска продукции, обеспечивающий максимальный доход от продаж, если спрос на вазы не превышает 200 шт. в неделю.
11. Изделия четырех типов проходят последовательную обработку на двух станках. Суточный фонд машинного времени каждого станка равен 10 часов. Время обработки и прибыль от продажи каждого изделия приведены в таблице.
| Изделие | Время обработки одного изделия, мин | ||
| Тип 1 | Тип 2 | Тип 3 | Тип 4 |
| Прибыль, $ |
Найти объем производства изделий каждого типа, позволяющий получить максимальную прибыль.
12. Завод выпускает изделия трех моделей – I, II и III. Для их изготовления используются два вида ресурсов. – А и В, запасы которых составляют 4000 и 6000 единиц соответственно. Расход ресурсов и прибыль на каждое изделие приведены в таблице.
| Ресурс | Расход ресурса на изделие | |
| I | II | III |
| А | ||
| В | ||
| Прибыль,$ |
Найти объем производства изделий каждого типа, позволяющий получить максимальную прибыль.
13. Фирма выпускает два типа автомобильных деталей (А и В). Для этого закупается литье, подвергаемое затем токарной обработке, сверлению и шлифованию. В таблице приведены параметры станочного парка фирмы.
| Станок | Деталь А, шт./ч | Деталь В, шт./ч |
| Токарный | ||
| Сверлильный | ||
| Шлифовальный |
Каждая отливка, из которой изготавливают деталь А, стоит 2$, а для детали В стоимость отливки равна 3$. Продажные цены деталей равны 5 и 6$. Стоимость часа станочного времени по указанным типам станков составляет 20, 14 и 17,5$. Определить план выпуска изделий, дающий максимальную прибыль.
14. Бройлерное хозяйство насчитывает 20000 цыплят. Для того, чтобы цыплята к моменту продажи достигли определенного веса, их кормовой рацион должен удовлетворять следующим требованиям:
– содержание кальция не менее 0,8% и не более 1,2%;
– содержание белка не менее 22%;
– содержание клетчатки не более 5%.
Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Пусть в распоряжении хозяйства имеются только ингредиенты, указанные в таблице. Там же указаны их параметры.
| Ингредиент | Содержание питательных веществ | Стоимость, $/кг | ||
| кальций | белок | клетчатка | ||
| Известняк | 0,38 | – | – | 0,04 |
| Зерно | 0,001 | 0,09 | 0,02 | 0,16 |
| Соевые бобы | 0,002 | 0,5 | 0,08 | 0,4 |
Необходимо составить кормовую смесь минимальной стоимости, содержание питательных веществ в которой удовлетворяет указанным выше требованиям.
Рекомендуемые страницы:
Источник
